Eigenvector Centrality (Centrality Measure)
Last Updated :
12 Feb, 2018
In graph theory, eigenvector centrality (also called eigencentrality) is a measure of the influence of a node in a network. It assigns relative scores to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes.
Google’s PageRank and the Katz centrality are variants of the eigenvector centrality.
Using the adjacency matrix to find eigenvector centrality
For a given graph
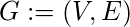
with
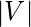
vertices let
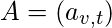
be the adjacency matrix, i.e.
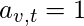
if vertex
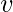
is linked to vertex
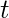
, and
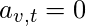
otherwise. The relative centrality score of vertex
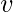
can be defined as:
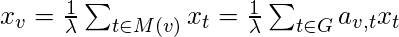
where
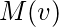
is a set of the neighbors of
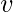
and
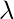
is a constant. With a small rearrangement this can be rewritten in vector notation as the eigenvector equation
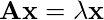
In general, there will be many different eigenvalues
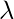
for which a non-zero eigenvector solution exists. However, the additional requirement that all the entries in the eigenvector be non-negative implies (by the Perron–Frobenius theorem) that only the greatest eigenvalue results in the desired centrality measure. The
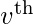
component of the related eigenvector then gives the relative centrality score of the vertex
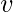
in the network. The eigenvector is only defined up to a common factor, so only the ratios of the centralities of the vertices are well defined. To define an absolute score one must normalise the eigen vector e.g. such that the sum over all vertices is 1 or the total number of vertices n. Power iteration is one of many eigenvalue algorithms that may be used to find this dominant eigenvector. Furthermore, this can be generalized so that the entries in A can be real numbers representing connection strengths, as in a stochastic matrix.

Following is the code for the calculation of the Eigen Vector Centrality of the graph and its various nodes.
def eigenvector_centrality(G, max_iter=100, tol=1.0e-6, nstart=None,
weight='weight'):
from math import sqrt
if type(G) == nx.MultiGraph or type(G) == nx.MultiDiGraph:
raise nx.NetworkXException("Not defined for multigraphs.")
if len(G) == 0:
raise nx.NetworkXException("Empty graph.")
if nstart is None:
x = dict([(n,1.0/len(G)) for n in G])
else:
x = nstart
s = 1.0/sum(x.values())
for k in x:
x[k] *= s
nnodes = G.number_of_nodes()
for i in range(max_iter):
xlast = x
x = dict.fromkeys(xlast, 0)
for n in x:
for nbr in G[n]:
x[nbr] += xlast[n] * G[n][nbr].get(weight, 1)
try:
s = 1.0/sqrt(sum(v**2 for v in x.values()))
except ZeroDivisionError:
s = 1.0
for n in x:
x[n] *= s
err = sum([abs(x[n]-xlast[n]) for n in x])
if err < nnodes*tol:
return x
raise nx.NetworkXError(
)
|
The above function is invoked using the networkx library and once the library is installed, you can eventually use it and the following code has to be written in python for the implementation of the eigen vector centrality of a node.
>>> import networkx as nx
>>> G = nx.path_graph(4)
>>> centrality = nx.eigenvector_centrality(G)
>>> print(['%s %0.2f'%(node,centrality[node]) for node in centrality])
|
The output of the above code is:
['0 0.37', '1 0.60', '2 0.60', '3 0.37']
|
The above result is a dictionary depicting the value of eigen vector centrality of each node. The above is an extension of my article series on the centrality measures. Keep networking!!!
References
You can read more about the same at
https://en.wikipedia.org/wiki/Eigenvector_centrality
http://networkx.readthedocs.io/en/networkx-1.10/index.html
Image Source
https://image.slidesharecdn.com/srspesceesposito-150425073726-conversion-gate01/95/network-centrality-measures-and-their-effectiveness-28-638.jpg?cb=1429948092
Share your thoughts in the comments
Please Login to comment...