Double Integral
Last Updated :
06 Jul, 2023
Integral calculus is a very important part of mathematics and has applications in various fields such as physics, chemistry, and space technology. Integrals can be of multiple kinds such as linear integral, double integral, triple integral, and so on. Linear integral integrates the equation with respect to one variable and in case two variables are present, we need to substitute the value of one variable in terms of the other. This technique becomes very difficult when we deal with multiple variables to calculate the areas and volumes under the curves. Double integral is very useful in such cases. In this article, we will learn about double integral in detail.
What is Double Integral?
Double Integral in mathematics uses integration with respect to two variables. We do not need to convert the complete equation into one variable for double integral. Instead, we can integrate the function with respect to two variables also. This is very helpful in the case of functions where we are provided with only one function and no relationship between the variables is defined. In such cases, we cannot substitute the value of one variable from the relation. Thus, we use double integral to integrate the function. Double integral is mainly used to calculate the area of 2D surfaces or curves in mathematics.
Definition of Double Integral
Double integral is defined as the integral of a function over an area represented as R2.
A double integral is represented as follows:
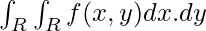
If the region R spans over an area of [a,b] and then the above equation can be written as:
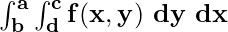
Here f(x, y) is a function of x and y, and the two integration signs represent the double integral over areas [a,b] and .
In the case of double integrals the inner integral is solved first and then we proceed to solve the outer integral. The calculation of the integral proceeds in the normal way by treating one variable at a time. In this case, the equation is integrated w.r.t x first, and then the equation is integrated w.r.t y.
How to Calculate Double Integral?
Steps to calculate the double integral are as follows:
Step 1: Write down the function to be integrated with a double integral sign and mention the upper and lower limits of integration on the integral.
Step 2: Integrate the function with respect to any one of the variables initially.
Step 3: Now plug the lower and upper limits of the variable with respect to which we integrated the function in order to bring the left function into one variable.
Step 4: Proceeding similarly as above, integrate the function again with respect to the other variable.
Step 5: Plug the lower and upper limits of the second variable to get the result.
Example: Consider the integration 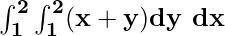 .
.
Solution:
In order to solve this integral, we will solve the inner integral first and integrate the function w.r.t x
Let 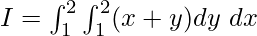
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2}{2}+xy]^{x=2}_{x=1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c22f20cad3e505137052104dc027990_l3.png)
Putting the upper and lower limits for x, we get
⇒ I ![Rendered by QuickLaTeX.com = \int^2_1[\frac{2^2}{2}+2y-(\frac{1^2}{2}+y)]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab22c0529682b4bdce6569411f950fdd_l3.png)
⇒ I ![Rendered by QuickLaTeX.com = \int^2_1[2+2y-\frac{1}{2}-y]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5690226086d3235e5997b7bb4abd2f14_l3.png)
⇒ I 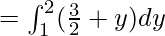
Now integrating w.r.t y, we get
⇒ I ![Rendered by QuickLaTeX.com = [\frac{3y}{2}+\frac{y^2}{2}]^{y=2}_{y=1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cccadf233a67d457ab6d6f82ade20bb_l3.png)
⇒ I ![Rendered by QuickLaTeX.com = [\frac{3(2)}{2}+\frac{2^2}{2}-(\frac{3(1)}{2}+\frac{1^2}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-67ed2031ffbc8e980d8d2f3af98501b8_l3.png)
⇒ I = 3 + 2 – 2 = 3
Volume using Double Integral
Volume using Double Integral is the geometric interpretation of the double integral, to calculate the volume using double integral, let’s consider a region R over [a x b] and . A curve S=f(x, y) is drawn such that it projects an area in this region R. The graph for this is shown below:
In order to calculate the volume of the shown region, we will divide the length cd of the area R into m equal parts and the breadth of the area R into n equal parts. Thus the complete area R gets divided into smaller rectangles. Now from each of these rectangles we will draw a box upwards to the point where it meets S. It can be shown as follows:
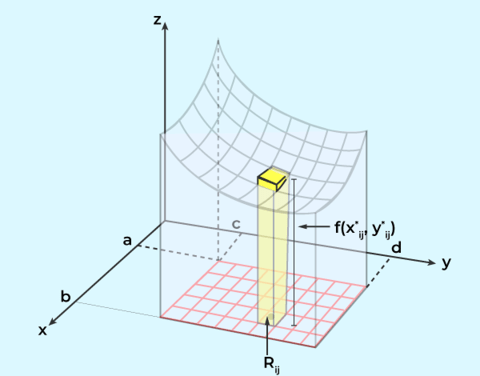
Consider that the area of the base of each small rectangle is A and its height is given by f(x’,y’). The volume under region S can be calculated using:
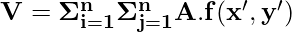
We have made use of two variables m and n because the volume will be added and calculated in both directions or axes i.e. X axis and Y axis. As the value of m and n becomes very large and approaches infinity which means the area R is divided into infinite small rectangular regions, then this equation can be written as:
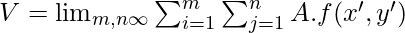
We know that when the variables tend to infinity then summation can be substituted with integration which is also the definition of integration. Thus above equation becomes equal to:
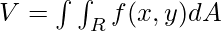
Thus we derive the formula to find the volume under the curve using a double integral.
Properties of Double Integral
Consider two functions f(x, y) and g(x, y) to be integrated over regions A and B respectively. Also, consider C and D to be sub-regions of A and B, then a double integral satisfies the following properties:
- Linearity:
![Rendered by QuickLaTeX.com \int \int_R[f(x,y)\pm g(x,y)] = \int \int_Rf(x,y)\pm\int \int_Rg(x,y)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c56c9d6fe68c49f71e351c5e7ffa998f_l3.png)
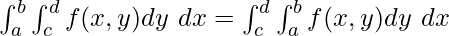
- Additivity: If
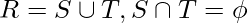 then,
then, 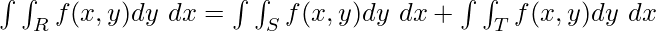
- Monotonicity: If f(x, y) ≥ g(x, y), then
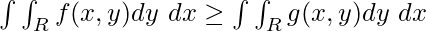
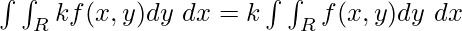
Solved Examples of Double Integral
Problem 1: Calculate 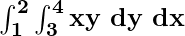 .
.
Solution:
Let 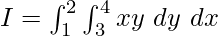
Putting the upper and lower limits for x, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy\\ \Rightarrow I = \int^2_1[\frac{4^2y}{2}-\frac{3^2y}{2}]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-efde547feac77853dac21fec6e1cfbd7_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \int^2_1\frac{7y}{2}dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d87fe1f0c6d2212fdf21658984d22adc_l3.png)
Now integrating w.r.t y, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = [\frac{7y^2}{4}]^{y=2}_{y=1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1df29321540b900f51f3f2486f47f61e_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = [\frac{7(2^2)}{4}-\frac{7(1^2)}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c314345a040ef3c5253165a989f2fa93_l3.png)
⇒ I = 7 – 7/4 = 21/4
Problem 2: Calculate 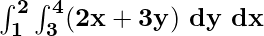 .
.
Solution:
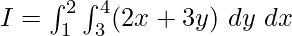
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{2x^2}{2}+3xy]^{x=4}_{x=3}dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cf5afdb5d2124370f53494545230474d_l3.png)
Putting the upper and lower limits for x, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \int^2_1[4^2+3(4)y-(3^2+3(3)y)]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68b885afe7d330d1334258b4ac90de86_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \int^2_1(16+12y -9-9y)dy = \int^2_1(7+3y)dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2e1783fa7d5151905b83179378660f3_l3.png)
Now integrating w.r.t y, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = [7y+ \frac{3y^2}{2}]^{y=2}_{y=1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d76ef0926c4edab31ec62a5c129b904_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = 7(2)+\frac{3(2^2)}{2}-(7(1)+\frac{3(1^2)}{2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec681f548adff1efcd807f7c17902023_l3.png)
⇒ I = 14 + 3 – 7 – 3/2 = 17/2
Problem 3: Calculate 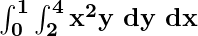 .
.
Solution:
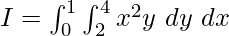
![Rendered by QuickLaTeX.com \Rightarrow I = \int^0_1[\frac{x^3y}{3}]^{x=4}_{x=2}dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb146efb74e176916f8a9c099495108f_l3.png)
Putting the upper and lower limits for x, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \int^1_0 (\frac{64y}{3}-\frac{8y}{3}) dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd41eafded1209c35351f4c7bc14a8af_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \int^1_0(\frac{56y}{3})dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e9c1c3206bf073c2da4a67b3b1af8316_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy \frac{56}{3}\int^1_0y~dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-21fa714484cf7d5b91ed2f0421d06083_l3.png)
Now integrating w.r.t y, we get
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \frac{56}{3}[\frac{y^2}{2}]^{y=1}_{y=0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce2c3ea27b866fe6ff91e7b82279f0ec_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = \frac{56}{3}(\frac{1}{2}-0)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e2a08697dd2ee69e0f21f7396e6d5d0_l3.png)
⇒ I = 56/6
Problem 4: Calculate 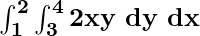 .
.
Solution:
Using 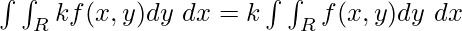
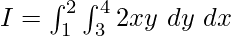
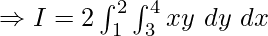
![Rendered by QuickLaTeX.com \Rightarrow I = \int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy = 2\int^2_1[\frac{x^2y}{2}]^{x=4}_{x=3}dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4eb6d214496fdaee091e61ee99feadcf_l3.png)
Putting the upper and lower limits for x, we get
![Rendered by QuickLaTeX.com \Rightarrow I= 2\int^2_1[\frac{4^2y}{2}-\frac{3^2y}{2}]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2b6eea4012bb2f574a762b61358af754_l3.png)
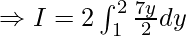
Now integrating w.r.t y, we get
![Rendered by QuickLaTeX.com \Rightarrow I= 2[\frac{7y^2}{4}]^{y=2}_{y=1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a96749f4842799575ddcd03abd4623d5_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I= 2[\frac{7(2^2)}{4}-\frac{7(1^2)}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c80b56a12f5374bb326edebf0a1506b8_l3.png)
⇒ I = 2(7 – 7/4) = 21/2
Problem 5: Calculate 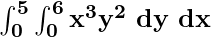 .
.
Solution:
Let 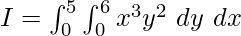
![Rendered by QuickLaTeX.com \Rightarrow I= \int^5_0[\frac{x^4y^2}{4}]^{x=6}_{x=0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea5f04a5302b95ec7a5c652160563253_l3.png)
Putting the upper and lower limits for x, we get
![Rendered by QuickLaTeX.com \Rightarrow I= \int^5_0[\frac{1296y^2}{4}-0]dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d894ccfe828b6e5f570cd2d5c2351db_l3.png)
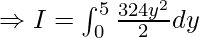
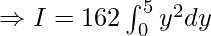
Now integrating w.r.t y, we get
![Rendered by QuickLaTeX.com \Rightarrow I= 162[\frac{y^3}{3}]^{y=5}_{y=0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68e4abcc5ceb62a630b8870e8ed2bf75_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow I= 162[\frac{125}{3}-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f44f7ee1684ded931139e17c53e9e315_l3.png)
⇒ I = 54(125) = 6750
FAQs of Double Integral
Q1: What is the Meaning of Double Integral?
Answer:
Double integral is the integration of a function with respect to two variables.
Q2: Can we Integrate the Double Integral using any of the Variables First?
Answer:
Yes, the double integral can be integrated by using any of the variables first as the order of integration of variables do not matter in case of a double integral.
Q3: What are Some Applications of Double Integral?
Answer:
Double integral is used to calculate the area and volume under one or more curves.
Q4: What is the Advantage of Double Integral over Single Integral?
Answer:
A single integral can be used only to calculate the area under a 2D curve but a double integral also helps us to calculate volume of a 3D curve.
Share your thoughts in the comments
Please Login to comment...