Divisibility by 3 where each digit is the sum of all prefix digits modulo 10
Last Updated :
19 Sep, 2022
Given K, number of digits, and d0 and d1 as the two digits to form the k-sized integer. Task is to check whether the k-sized number formed using d0 and d1 is divisible by 3 or not.
For each i, di is the sum of all preceding (more significant) digits, modulo 10 — more formally, the following formula must hold :
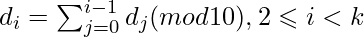
Examples :
Input : K = 5 d0 = 3 d1 = 4
Output : NO
Explanation :
The whole number N is 34748 (Starting from
third digit, every digit is some of preceding
digits mod 10). Since 34748 is not divisible
by 3, answer is NO.
Input : K = 13 d0 = 8 d1 = 1
Output : YES
Explanation :
The whole number N is 8198624862486,
which is divisible by 3, so the answer
is YES.
K may be very long so generating the entire number, calculating the sum of digits and then checking for multiple of 3 is cumbersome. The key idea behind the solution is that the digits start repeating after some time in a cycle of length 4 and then the sum of digits can be determined in O(1) step.
We know d0 and d1,
So, d2 = (d0 + d1) mod 10
d3 = (d2 + d1 + d0) mod 10 = ((d0 + d1) mod 10 + (d0 + d1)) mod 10 = 2 * (d0 + d1) mod 10
d4 = (d3 + d2 + d1 + d0) mod 10 = 4 * (d0 + d1) mod 10
d5 = (d4 + d3 + d2 + d1 + d0) mod 10 = 8 * (d0 + d1) mod 10
d6 = (d5 +…+ d1 + d0) mod 10 = 16 * (d0 + d1) mod 10 = 6 * (d0 + d1) mod 10
d7 = (d6 +…+ d1 + d0) mod 10 = 32 * (d0 + d1) mod 10 = 2 * (d0 + d1) mod 10
If we keep on getting di, we will see that the resultant is just looping through the same values. We can see that (d0 + d1) contributes 1 time(s) to d2, 2 times to d3, 4 times to d4, 8 times to d5, …, 2^(k – 2) times to dk.
But, since the powers of 2 under modulo 10 cycle from 1, 2, 4, 8, 6, 2, 4. Here, the cycle length is of 4, where d2 is not present in the cycle. Let, S = (2 * (d0 + d1)) mod 10 + (4 * (d0 + d1)) mod 10 + (8 * (d0 + d1)) mod 10 + (6 * (d0 + d1)) mod 10, this is the cycle which repeats.
So, the sum of digits = (d0 + d1 + d2) + S * ( (k – 3) / 4 ) + x. Here, the first 3 terms will be covered by d0, d1, d2 and after that the groups of 4 will be covered by S, but this formula will still has not summed some terms at the end. That is the residue that is noted by x.
Below is the implementation of above approach :
C++
#include <bits/stdc++.h>
using namespace std;
string check(long int k, int d0, int d1)
{
long int s = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10 +
(6 * (d0 + d1)) % 10;
int a = (k - 3) % 4;
int x;
switch(a)
{
case 0:
x = 0;
break;
case 1:
x = (2 * (d0 + d1)) % 10;
break;
case 2:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10;
break;
case 3:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10;
break;
}
long int sum = d0 + d1 + ((k - 3) / 4) * s + x;
if(sum % 3 == 0)
return "YES";
return "NO";
}
int main()
{
long int k, d0, d1;
k = 13;
d0 = 8;
d1 = 1;
cout << check(k, d0, d1) << endl;
k = 5;
d0 = 3;
d1 = 4;
cout << check(k, d0, d1) << endl;
return 0;
}
|
Java
import java.util.*;
import java.io.*;
class GFG {
static String check( int k, int d0, int d1)
{
int s = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10 +
(6 * (d0 + d1)) % 10;
int a = (k - 3) % 4;
int x=0;
switch(a)
{
case 0:
x = 0;
break;
case 1:
x = (2 * (d0 + d1)) % 10;
break;
case 2:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10;
break;
case 3:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10;
break;
}
int sum = d0 + d1 + (((k - 3) / 4) * s + x );
if(sum % 3 == 0)
return "YES";
return "NO";
}
public static void main (String[] args) {
int k, d0, d1;
k = 13;
d0 = 8;
d1 = 1;
System.out.println (check(k, d0, d1));
k = 5;
d0 = 3;
d1 = 4;
System.out.println (check(k, d0, d1));
}
}
|
Python3
def check(k, d0, d1):
s = ((2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10 +
(6 * (d0 + d1)) % 10)
a = (k - 3) % 4
if(a == 0):
x = 0
elif(a == 1):
x = (2 * (d0 + d1)) % 10
elif(a == 2):
x = ((2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10)
elif(a == 3):
x = ((2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10)
sum = d0 + d1 + ((k - 3) // 4) * s + x
if(sum % 3 == 0):
return "YES"
else:
return "NO"
if __name__=='__main__':
k = 13
d0 = 8
d1 = 1
print(check(k, d0, d1))
k = 5
d0 = 3
d1 = 4
print(check(k, d0, d1))
|
C#
using System;
class GFG
{
static String check(int k, int d0, int d1)
{
int s = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10 +
(6 * (d0 + d1)) % 10;
int a = (k - 3) % 4;
int x = 0;
switch(a)
{
case 0:
x = 0;
break;
case 1:
x = (2 * (d0 + d1)) % 10;
break;
case 2:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10;
break;
case 3:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10;
break;
}
int sum = d0 + d1 + (((k - 3) / 4) * s + x );
if(sum % 3 == 0)
return "YES";
return "NO";
}
static public void Main ()
{
int k, d0, d1;
k = 13;
d0 = 8;
d1 = 1;
Console.WriteLine (check(k, d0, d1));
k = 5;
d0 = 3;
d1 = 4;
Console.WriteLine(check(k, d0, d1));
}
}
|
PHP
<?php
function check($k, $d0,$d1)
{
$s = (2 * ($d0 + $d1)) % 10 +
(4 * ($d0 + $d1)) % 10 +
(8 * ($d0 + $d1)) % 10 +
(6 * ($d0 + $d1)) % 10;
$a = ($k - 3) % 4;
$x;
switch($a)
{
case 0:
$x = 0;
break;
case 1:
$x = (2 * ($d0 +
$d1)) % 10;
break;
case 2:
$x = (2 * ($d0 + $d1)) % 10 +
(4 * ($d0 + $d1)) % 10;
break;
case 3:
$x = (2 * ($d0 + $d1)) % 10 +
(4 * ($d0 + $d1)) % 10 +
(8 * ($d0 + $d1)) % 10;
break;
}
$sum = $d0 + $d1 +
(int)(($k - 3) /
4) * $s + $x;
if($sum % 3 == 0)
return "YES";
return "NO";
}
$k; $d0; $d1;
$k = 13;
$d0 = 8;
$d1 = 1;
echo check($k, $d0, $d1), "\n";
$k = 5;
$d0 = 3;
$d1 = 4;
echo check($k, $d0, $d1), "\n";
?>
|
Javascript
<script>
function check(k, d0,d1)
{
let s = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10 +
(6 * (d0 + d1)) % 10;
let a = (k - 3) % 4;
let x;
switch(a)
{
case 0:
x = 0;
break;
case 1:
x = (2 * (d0 +
d1)) % 10;
break;
case 2:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10;
break;
case 3:
x = (2 * (d0 + d1)) % 10 +
(4 * (d0 + d1)) % 10 +
(8 * (d0 + d1)) % 10;
break;
}
let sum = d0 + d1 +
parseInt((k - 3) /
4) * s + x;
if(sum % 3 == 0)
return "YES";
return "NO";
}
let k, d0, d1;
k = 13;
d0 = 8;
d1 = 1;
document.write(check(k, d0, d1) + "<br>");
k = 5;
d0 = 3;
d1 = 4;
document.write(check(k, d0, d1) + "<br>");
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...