Direction of a Point from a Line Segment
Last Updated :
18 Jun, 2022
Direction of given point P from a line segment simply means given the co-ordinates of a point P and line segment (say AB), and we have to determine the direction of point P from the line segment. That is whether the Point lies to the Right of Line Segment or to the Left of Line Segment.
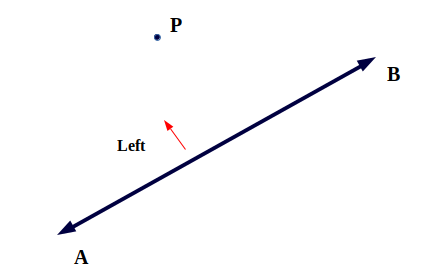
The point might lie behind the line segment, in that case we assume imaginary line by extending the line segment and determine the direction of point.

* There are only three cases, either the point is on left side, or right side or on the line segment itself.
This is a very fundamental Problem and is commonly encountered for directions in online map,
Example : Suppose a user A has to go to Point C in the following map, the user first reaches point B but after that how does user A know that whether he has to make a right turn or left turn.

Knowing the direction of a point from a line segment also acts a building block to solve more complicated problem such as :
- Line segment Intersection : finding if two line segment intersect
- Convex Hull of a set of Points.
The co-ordinate system we’ll use is a cartesian plane, as most 2-Dimensional problem uses cartesian plane and since this is a 2-Dimensional Problem.
This Problem can be solved using cross-product of vector algebra
Cross-Product of two point A and B is : Ax * By – Ay * Bx
where Ax and Ay are x and y co-ordinates of A respectively. Similarly Bx and By are x and y co-ordinates of B respectively.
The Cross-Product has an interesting Property which will be used to determine direction of a point from a line segment. That is, the cross-product of two points is positive if and only if the angle of those point at origin (0, 0) is in counter-clockwise. And conversely the cross-product is negative if and only if the angle of those point at origin is in clockwise direction.
An example would certainly clarify it,
In the following figure, the angle BOP is anti-clockwise and the cross-product of B X P = 29*28 – 15*(-15) = 1037 which is positive.

This helps us to make a conclusion that a point on right side must a have positive cross-product and a point on left side must have a negative cross product. Also note that we assumed one point of line segment to be origin and hence we need to convert any three point system such that one point of line segment is origin.
Following example explains the concept :
The three point A, B and P were converted into A’, B’ and P’ so as to make A as origin (this can be simply done by subtracting co-ordinates of A from point P and B), and then calculate the cross-product : 59*18 – (-25)*18 = 2187
Since this is positive, the Point P is on right side of line Segment AB.

C++
#include <iostream>
using namespace std;
struct point {
int x, y;
};
const int RIGHT = 1, LEFT = -1, ZERO = 0;
int directionOfPoint(point A, point B, point P)
{
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
int cross_product = B.x * P.y - B.y * P.x;
if (cross_product > 0)
return RIGHT;
if (cross_product < 0)
return LEFT;
return ZERO;
}
int main()
{
point A, B, P;
A.x = -30;
A.y = 10;
B.x = 29;
B.y = -15;
P.x = 15;
P.y = 28;
int direction = directionOfPoint(A, B, P);
if (direction == 1)
cout << "Right Direction" << endl;
else if (direction == -1)
cout << "Left Direction" << endl;
else
cout << "Point is on the Line" << endl;
return 0;
}
|
Java
class GFG
{
static class point
{
int x, y;
};
static int RIGHT = 1, LEFT = -1, ZERO = 0;
static int directionOfPoint(point A,
point B, point P)
{
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
int cross_product = B.x * P.y - B.y * P.x;
if (cross_product > 0)
return RIGHT;
if (cross_product < 0)
return LEFT;
return ZERO;
}
public static void main(String[] args)
{
point A = new point(),
B = new point(), P = new point();
A.x = -30;
A.y = 10;
B.x = 29;
B.y = -15;
P.x = 15;
P.y = 28;
int direction = directionOfPoint(A, B, P);
if (direction == 1)
System.out.println("Right Direction");
else if (direction == -1)
System.out.println("Left Direction");
else
System.out.println("Point is on the Line");
}
}
|
Python3
class point:
def __init__(self):
self.x = 0
self.y = 0
RIGHT = 1
LEFT = -1
ZERO = 0
def directionOfPoint(A, B, P):
global RIGHT, LEFT, ZERO
B.x -= A.x
B.y -= A.y
P.x -= A.x
P.y -= A.y
cross_product = B.x * P.y - B.y * P.x
if (cross_product > 0):
return RIGHT
if (cross_product < 0):
return LEFT
return ZERO
if __name__=="__main__":
A = point()
B = point()
P = point()
A.x = -30
A.y = 10
B.x = 29
B.y = -15
P.x = 15
P.y = 28
direction = directionOfPoint(A, B, P)
if (direction == 1):
print("Right Direction")
elif (direction == -1):
print("Left Direction")
else:
print("Point is on the Line")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class point
{
public int x, y;
};
static int RIGHT = 1, LEFT = -1, ZERO = 0;
static int directionOfPoint(point A,
point B, point P)
{
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
int cross_product = B.x * P.y - B.y * P.x;
if (cross_product > 0)
return RIGHT;
if (cross_product < 0)
return LEFT;
return ZERO;
}
public static void Main(String[] args)
{
point A = new point(),
B = new point(),
P = new point();
A.x = -30;
A.y = 10;
B.x = 29;
B.y = -15;
P.x = 15;
P.y = 28;
int direction = directionOfPoint(A, B, P);
if (direction == 1)
Console.WriteLine("Right Direction");
else if (direction == -1)
Console.WriteLine("Left Direction");
else
Console.WriteLine("Point is on the Line");
}
}
|
Javascript
<script>
class point
{
constructor()
{
this.x=0;
this.y=0;
}
}
let RIGHT = 1, LEFT = -1, ZERO = 0;
function directionOfPoint(A,B,P)
{
B.x -= A.x;
B.y -= A.y;
P.x -= A.x;
P.y -= A.y;
let cross_product = B.x * P.y - B.y * P.x;
if (cross_product > 0)
return RIGHT;
if (cross_product < 0)
return LEFT;
return ZERO;
}
let A = new point(),
B = new point(), P = new point();
A.x = -30;
A.y = 10;
B.x = 29;
B.y = -15;
P.x = 15;
P.y = 28;
let direction = directionOfPoint(A, B, P);
if (direction == 1)
document.write("Right Direction<br>");
else if (direction == -1)
document.write("Left Direction");
else
document.write("Point is on the Line");
</script>
|
Output:
Right Direction
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...