Different possible marks for n questions and negative marking
Last Updated :
08 Sep, 2022
Given the number of questions as 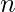 , and marks for the correct answer as
, and marks for the correct answer as 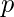 and
and 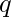 marks for the incorrect answer. One can either attempt to solve the question in an examination and get either
marks for the incorrect answer. One can either attempt to solve the question in an examination and get either 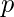 marks if the answer is right, or
marks if the answer is right, or 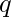 marks if the answer is wrong, or leave the question unattended and get
marks if the answer is wrong, or leave the question unattended and get 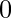 marks. The task is to find the count of all the different possible marks that one can score in the examination.
marks. The task is to find the count of all the different possible marks that one can score in the examination.
Examples:
Input: n = 2, p = 1, q = -1
Output: 5
The different possible marks are: -2, -1, 0, 1, 2
Input: n = 4, p = 2, q = -1
Output: 12
Approach: Iterate through all the possible number of correctly solved and unsolved problems. Store the scores in a set containing distinct elements keeping in mind that there is a positive number of incorrectly solved problems.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int scores(int n, int p, int q)
{
set<int> hset;
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
int correct = i;
int not_solved = j;
int incorrect = n - i - j;
if (incorrect >= 0)
hset.insert(p * correct
+ q * incorrect);
else
break;
}
}
return hset.size();
}
int main()
{
int n = 4;
int p = 2;
int q = -1;
cout << (scores(n, p, q));
}
|
Java
import java.util.*;
class GFG {
static int scores(int n, int p, int q)
{
HashSet<Integer>
hset = new HashSet<Integer>();
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= n; j++) {
int correct = i;
int not_solved = j;
int incorrect = n - i - j;
if (incorrect >= 0)
hset.add(p * correct
+ q * incorrect);
else
break;
}
}
return hset.size();
}
public static void main(String[] args)
{
int n = 4;
int p = 2;
int q = -1;
System.out.println(scores(n, p, q));
}
}
|
Python3
def scores(n, p, q):
hset = set()
for i in range(0, n + 1):
for j in range(0, n + 1):
correct = i
not_solved = j
incorrect = n - i - j
if incorrect >= 0:
hset.add(p * correct +
q * incorrect)
else:
break
return len(hset)
if __name__ == "__main__":
n = 4
p = 2
q = -1
print(scores(n, p, q))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int scores(int n, int p, int q)
{
HashSet<int>
hset = new HashSet<int>();
for (int i = 0; i <= n; i++)
{
for (int j = 0; j <= n; j++)
{
int correct = i;
int not_solved = j;
int incorrect = n - i - j;
if (incorrect >= 0)
hset.Add(p * correct
+ q * incorrect);
else
break;
}
}
return hset.Count;
}
public static void Main()
{
int n = 4;
int p = 2;
int q = -1;
Console.WriteLine(scores(n, p, q));
}
}
|
Javascript
<script>
function scores(n, p, q)
{
let hset = new Set();
for (let i = 0; i <= n; i++) {
for (let j = 0; j <= n; j++) {
let correct = i;
let not_solved = j;
let incorrect = n - i - j;
if (incorrect >= 0)
hset.add(p * correct
+ q * incorrect);
else
break;
}
}
return hset.size;
}
let n = 4;
let p = 2;
let q = -1;
document.write(scores(n, p, q));
</script>
|
Share your thoughts in the comments
Please Login to comment...