Determining Countability in TOC
Last Updated :
27 Nov, 2019
Countable Set is a set having cardinality same as that of some subset of
N the set of natural numbers . A countable set is the one which is listable.
Cardinality of a countable set can be a finite number. For example, B: {1, 5, 4}, |B| = 3, in this case its termed countably finite or the cardinality of countable set can be infinite. For example, A: {2, 4, 6, 8 …}, in this case its termed countably infinite.
Common Traces for Countable Set:
- Cardinality expressed in form
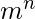 where
where 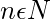 ,
, 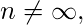 ; m may or may not be ∞
; m may or may not be ∞
- It has finite elements* only in case of countably finite sets.
- It listable in terms of roaster form* an exhaustive list exists which can include every element atleast once, in case of countably infinite list first few elements followed by three dot ellipsis(…).
Set of Rational numbers is Countably Infinite:
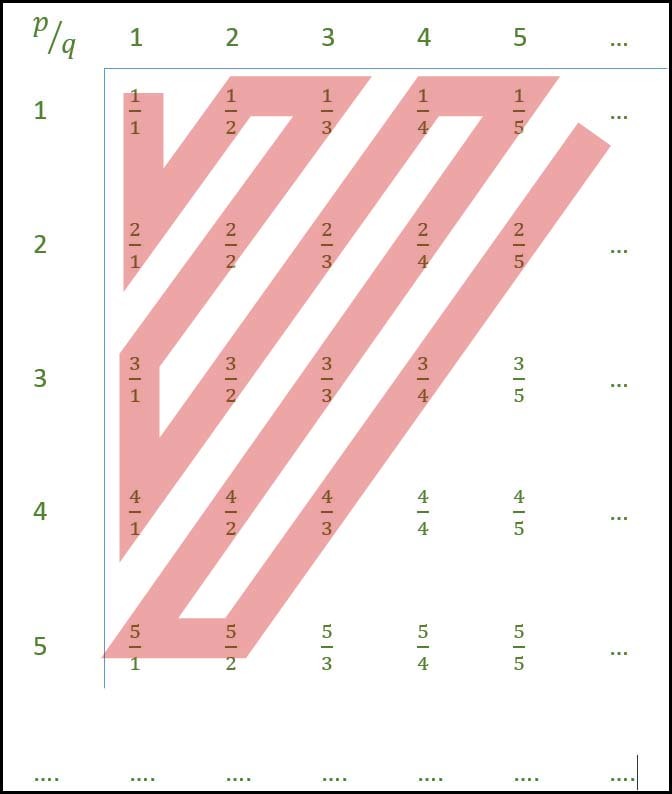
Follow along the red line to build roaster set containing all rational numbers. Hence an exhaustive set containing every element atleast once can be build therefore set of rational numbers is countably infinite.
Uncountable Sets:
A set such that its elements cannot be listed, or to put intuitively, there exists no sequence which can list every element of the set atleast once.
Example:
R : {set of real numbers is uncountable}
B : {set of all binary sequences of infinite length}
Common Traces for Uncountable Set:
- Cardinality expressed in form
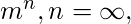 ;
;
- It is power set of set with infinite elements
- It is equal set to R set of real numbers
- It is equal set to Q set of irrational numbers
- It is non-listable set
Union Operations quick Reference:
| A |
B |
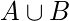 |
| Countable |
Countable |
Countable |
| Uncountable |
Uncountable |
Uncountable |
| Countable |
Uncountable |
Uncountable |
Example-1:
Let N be the set of natural numbers. Consider the following sets,
P: Set of Rational numbers (positive and negative)
Q: Set of functions from {0, 1} to N
R: Set of functions from N to {0, 1}
S: Set of finite subsets of N
Which of the above sets are countable ?
(A) Q and S only
(B) P and S only
(C) P and R only
(D) P, Q and S only
Explanation:
Please see
GATE CS 2018 | Question 58
Example-2:
Consider the following sets:
S1: Set of all recursively enumerable languages over the alphabet {0, 1}.
S2: Set of all syntactically valid C programs.
S3: Set of all languages over the alphabet {0, 1}.
S4: Set of all non-regular languages over the alphabet {0, 1}.
Which of the above sets are uncountable?
(A) S1 and S2
(B) S3 and S4
(C) S1 and S4
(D) S2 and S3
Explanation:
Please see
GATE CS 2019 | Question 43
Share your thoughts in the comments
Please Login to comment...