Count the numbers which can convert N to 1 using given operation
Last Updated :
08 Nov, 2021
Given a positive integer N (N ? 2), the task is to count the number of integers X in the range [2, N] such that X can be used to convert N to 1 using the following operation:
- If N is divisible by X, then update N’s value as N / X.
- Else, update N’s value as N – X.
Examples:
Input: N = 6
Output: 3
Explanation:
The following integers can be used to convert N to 1:
X = 2 => N = 6 -> N = 3 -> N = 1
X = 5 => N = 6 -> N = 1
X = 6 => N = 6 -> N = 1
Input: N = 48
Output: 4
Naive Approach: The naive approach for this problem is to iterate through all the integers from 2 to N and count the number of integers that can convert N to 1.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countValues(int n)
{
int answer = 0;
for (int i = 2; i <= n; i++) {
int k = n;
while (k >= i) {
if (k % i == 0)
k /= i;
else
k -= i;
}
if (k == 1)
answer++;
}
return answer;
}
int main()
{
int N = 6;
cout << countValues(N);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static int countValues(int n)
{
int answer = 0;
for (int i = 2; i <= n; i++)
{
int k = n;
while (k >= i)
{
if (k % i == 0)
k /= i;
else
k -= i;
}
if (k == 1)
answer++;
}
return answer;
}
public static void main(String args[])
{
int N = 6;
System.out.print(countValues(N));
}
}
|
Python3
def countValues(n):
answer = 0
for i in range(2, n + 1, 1):
k = n
while (k >= i):
if (k % i == 0):
k //= i
else:
k -= i
if (k == 1):
answer += 1
return answer
if __name__ == '__main__':
N = 6
print(countValues(N))
|
C#
using System;
class GFG{
static int countValues(int n)
{
int answer = 0;
for (int i = 2; i <= n; i++)
{
int k = n;
while (k >= i)
{
if (k % i == 0)
k /= i;
else
k -= i;
}
if (k == 1)
answer++;
}
return answer;
}
public static void Main()
{
int N = 6;
Console.Write(countValues(N));
}
}
|
Javascript
<script>
function countValues(n)
{
let answer = 0;
for (let i = 2; i <= n; i++) {
let k = n;
while (k >= i) {
if (k % i == 0)
k /= i;
else
k -= i;
}
if (k == 1)
answer++;
}
return answer;
}
let N = 6;
document.write(countValues(N));
</script>
|
Time Complexity: O(N), where N is the given number.
Auxiliary Space: O(1)
Efficient Approach: The idea is to observe that if N is not divisible by X initially, then only the subtraction will be carried throughout as after each subtraction N still wouldn’t be divisible by N. Also these operations will stop when N ? X, and the final value of N will be equal to N mod X.
So, for all the numbers from 2 to N, there are only two possible cases :
- No division operation occurs: For all these numbers, the final value will be equal to N mod X. N will become one in the end only if N mod X = 1. Clearly, for X = N – 1, and all divisors of N – 1, N mod X = 1 holds true.
- Division operation occurs more than once: Division operation will only occur for divisors on N. For each divisor of N say d, perform the division till N mod d != 0. If finally N mod d = 1, then this will be included in the answer else not (using the property derived from Case 1).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countValues(int N)
{
vector<int> div;
for (int i = 2; i * i <= N; i++) {
if (N % i == 0) {
div.push_back(i);
if (N != i * i) {
div.push_back(N / i);
}
}
}
int answer = 0;
for (int i = 1; i * i <= N - 1; i++) {
if ((N - 1) % i == 0) {
if (i * i == N - 1)
answer++;
else
answer += 2;
}
}
for (auto d : div) {
int K = N;
while (K % d == 0)
K /= d;
if ((K - 1) % d == 0)
answer++;
}
return answer;
}
int main()
{
int N = 6;
cout << countValues(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int countValues(int N)
{
Vector<Integer> div = new Vector<>();
for(int i = 2; i * i <= N; i++)
{
if (N % i == 0)
{
div.add(i);
if (N != i * i)
{
div.add(N / i);
}
}
}
int answer = 0;
for(int i = 1; i * i <= N - 1; i++)
{
if ((N - 1) % i == 0)
{
if (i * i == N - 1)
answer++;
else
answer += 2;
}
}
for(int d : div)
{
int K = N;
while (K % d == 0)
K /= d;
if ((K - 1) % d == 0)
answer++;
}
return answer;
}
public static void main(String[] args)
{
int N = 6;
System.out.print(countValues(N));
}
}
|
Python3
def countValues(N):
div = []
i = 2
while ((i * i) <= N):
if (N % i == 0):
div.append(i)
if (N != i * i):
div.append(N // i)
i += 1
answer = 0
i = 1
while((i * i) <= N - 1):
if ((N - 1) % i == 0):
if (i * i == N - 1):
answer += 1
else:
answer += 2
i += 1
for d in div:
K = N
while (K % d == 0):
K //= d
if ((K - 1) % d == 0):
answer += 1
return answer
if __name__=="__main__":
N = 6
print(countValues(N))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int countValues(int N)
{
List<int> div = new List<int>();
for(int i = 2; i * i <= N; i++)
{
if (N % i == 0)
{
div.Add(i);
if (N != i * i)
{
div.Add(N / i);
}
}
}
int answer = 0;
for(int i = 1; i * i <= N - 1; i++)
{
if ((N - 1) % i == 0)
{
if (i * i == N - 1)
answer++;
else
answer += 2;
}
}
foreach(int d in div)
{
int K = N;
while (K % d == 0)
K /= d;
if ((K - 1) % d == 0)
answer++;
}
return answer;
}
public static void Main(String[] args)
{
int N = 6;
Console.Write(countValues(N));
}
}
|
Javascript
<script>
function countValues(N)
{
var div = [];
for (var i = 2; i * i <= N; i++) {
if (N % i == 0) {
div.push(i);
if (N != i * i) {
div.push(N / i);
}
}
}
var answer = 0;
for (var i = 1; i * i <= N - 1; i++) {
if ((N - 1) % i == 0) {
if (i * i == N - 1)
answer++;
else
answer += 2;
}
}
div.forEach(d => {
var K = N;
while (K % d == 0)
K /= d;
if ((K - 1) % d == 0)
answer++;
});
return answer;
}
var N = 6;
document.write( countValues(N));
</script>
|
Time Complexity:
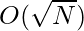
Auxiliary Space: O(sqrt(N))
Share your thoughts in the comments
Please Login to comment...