Count permutations that are first decreasing then increasing.
Last Updated :
21 Aug, 2022
Given an integer N, calculate the number of permutations of A = [1, 2, …, N] which are first decreasing and then increasing.
Examples:
Input: N = 5
Output : 14
Following are the sub-sequences which are first decreasing and then increasing:
[2, 1, 3, 4, 5], [3, 1, 2, 4, 5], [4, 1, 2, 3, 5], [5, 1, 2, 3, 4],
[3, 2, 1, 4, 5], [4, 2, 1, 3, 5], [5, 2, 1, 3, 4], [4, 3, 1, 2, 5],
[5, 3, 1, 2, 4], [5, 4, 1, 2, 3], [5, 4, 3, 1, 2], [5, 4, 2, 1, 3],
[5, 3, 2, 1, 4], [4, 3, 2, 1, 5]
Input : N = 1
Output : 0
Approach: It is clear that the point at which sequence becomes increasing from decreasing is occupied by the smallest element of the permutation which is 1. Also, decreasing sequence is always followed by an increasing sequence which means that the smallest element can have positions ranging [2, …, N-1]. Otherwise, it will result in a fully increasing or fully decreasing sequence.
For example, consider N = 5 and position = 2, i.e the smallest element at position 2 in the sequence. Count all possible sequences with Configuration = [_, 1, _, _, _].
Select any 1 element from the remaining 4 elements (2, 3, 4, 5) to fill position 1. For example, we select element = 3. The configuration looks like [3, 1, _, _, _]. Only 1 sequence is possible i.e [3, 1, 2, 4, 5]. Thus, for every selected element to fill position 1, a sequence is possible. With this configuration, a total of 4C1 permutations is possible.
Now, consider the configuration = [_, _, 1, _, _].
A similar approach can be applied by selecting any 2 elements from the remaining 4 elements and for every pair of elements, a single valid permutation is possible. Hence, the number of permutations for this configuration = 4C2
The final configuration possible for N = 5 is [_, _, _, 1, _]
Select any 3 of the remaining 4 elements and for every triplet, a permutation is obtained. Number of permutations, in this case, = 4C3
Final count = 4C1 + 4C2 + 4C3 for N = 5
Generalized result for N:
Count = N-1C1 + N-1C2 + ... + N-1CN-2 which simplifies to,
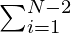 N-1Ci = 2N-1 - 2 (from binomial theorem)
N-1Ci = 2N-1 - 2 (from binomial theorem)
C++
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 1000000007;
ll power(ll a, ll n)
{
if (n == 0)
return 1;
ll p = power(a, n / 2) % mod;
p = (p * p) % mod;
if (n & 1)
p = (p * a) % mod;
return p;
}
int countPermutations(int n)
{
if (n == 1) {
return 0;
}
return (power(2, n - 1) - 2) % mod;
}
int main()
{
int n = 5;
cout << countPermutations(n);
return 0;
}
|
Java
class GFG
{
static final int mod = 1000000007;
static long power(long a, long n)
{
if (n == 0)
return 1;
long p = power(a, n / 2) % mod;
p = (p * p) % mod;
if ((n & 1) == 1)
p = (p * a) % mod;
return p;
}
static int countPermutations(int n)
{
if (n == 1)
{
return 0;
}
return ((int)power(2, n - 1) - 2) % mod;
}
public static void main(String args[])
{
int n = 5;
System.out.println(countPermutations(n));
}
}
|
Python3
mod = 1000000007
def power(a, n):
if(n == 0):
return 1
p = power(a, int(n / 2)) % mod;
p = (p * p) % mod
if (n & 1):
p = (p * a) % mod
return p
def countPermutations(n):
if (n == 1):
return 0
return (power(2, n - 1) - 2) % mod
if __name__ == '__main__':
n = 5
print(countPermutations(n))
|
C#
using System;
class GFG
{
static int mod = 1000000007;
static long power(long a, long n)
{
if (n == 0)
return 1;
long p = power(a, n / 2) % mod;
p = (p * p) % mod;
if ((n & 1) == 1)
p = (p * a) % mod;
return p;
}
static int countPermutations(int n)
{
if (n == 1)
{
return 0;
}
return ((int)power(2, n - 1) - 2) % mod;
}
static public void Main ()
{
int n = 5;
Console.WriteLine(countPermutations(n));
}
}
|
PHP
<?php
$mod = 1000000007;
function power($a, $n)
{
global $mod;
if ($n == 0)
return 1;
$p = power($a, $n / 2) % $mod;
$p = ($p * $p) % $mod;
if ($n & 1)
$p = ($p * $a) % $mod;
return $p;
}
function countPermutations($n)
{
global $mod;
if ($n == 1)
{
return 0;
}
return (power(2, $n - 1) - 2) % $mod;
}
$n = 5;
echo countPermutations($n);
?>
|
Javascript
<script>
let mod = 1000000007;
function power(a, n)
{
if (n == 0)
return 1;
let p = power(a, parseInt(n / 2, 10)) % mod;
p = (p * p) % mod;
if ((n & 1) == 1)
p = (p * a) % mod;
return p;
}
function countPermutations(n)
{
if (n == 1)
{
return 0;
}
return (power(2, n - 1) - 2) % mod;
}
let n = 5;
document.write(countPermutations(n));
</script>
|
Time Complexity: O(log2n)
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...