Count of values of x <= n for which (n XOR x) = (n – x)
Last Updated :
19 Sep, 2022
Given an integer n, the task is to find the number of possible values of 0 ? x ? n which satisfy n XOR x = n – x.
Examples:
Input: n = 5
Output: 4
Following values of x satisfy the equation
5 XOR 0 = 5 – 0 = 5
5 XOR 1 = 5 – 1 = 4
5 XOR 4 = 5 – 4 = 1
5 XOR 5 = 5 – 5 = 0
Input: n = 2
Output: 2
Naive approach: The easy approach is to check for all values from 0 to n (both inclusive) and finding whether they satisfy the equation. The below code implements this approach:
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
static int countX(int n)
{
int count = 0;
for (int i = 0; i <= n; i++)
{
if (n - i == (n ^ i))
count++;
}
return count;
}
int main()
{
int n = 5;
int answer = countX(n);
cout << answer;
}
|
Java
public class GFG {
static int countX(int n)
{
int count = 0;
for (int i = 0; i <= n; i++) {
if (n - i == (n ^ i))
count++;
}
return count;
}
public static void main(String args[])
{
int n = 5;
int answer = countX(n);
System.out.println(answer);
}
}
|
Python3
import math as mt
def countX(n):
count = 0
for i in range(n + 1):
if n - i == (n ^ i):
count += 1
return count
if __name__ == '__main__':
n = 5
answer = countX(n)
print(answer)
|
C#
using System;
class GFG
{
static int countX(int n)
{
int count = 0;
for (int i = 0; i <= n; i++)
{
if (n - i == (n ^ i))
count++;
}
return count;
}
public static void Main()
{
int n = 5;
int answer = countX(n);
Console.WriteLine(answer);
}
}
|
PHP
<?php
function countX($n)
{
$count = 0;
for ($i = 0; $i <= $n; $i++)
{
if ($n - $i == ($n ^ $i))
$count++;
}
return $count;
}
$n = 5;
$answer = countX($n);
echo($answer);
?>
|
Javascript
<script>
function countX(n)
{
let count = 0;
for (let i = 0; i <= n; i++)
{
if (n - i == (n ^ i))
count++;
}
return count;
}
let n = 5;
let answer = countX(n);
document.write(answer);
</script>
|
Time complexity: O(N)
Auxiliary Space: O(1)
Efficient Approach: Convert n to its binary representation. Now, for every 1 in the binary string whether we subtract 1 or 0 from it, it will be equivalent to XOR of 1 with 0 or 1 i.e.
(1 – 1) = (1 XOR 1) = 0
(1 – 0) = (1 XOR 0) = 1
But 0 doesn’t satisfy this condition. So, we only need to consider all the ones in the binary representation of n. Now, for every 1 there are two possibilities, either 0 or 1. Thus if we have m number of 1’s in n then our solution would be 2m.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
int countX(int n)
{
string binary = bitset<8>(n).to_string();
int count = 0;
for (int i = 0; i < binary.length(); i++)
{
if (binary.at(i) == '1')
count++;
}
int answer = (int)pow(2, count);
return answer;
}
int main()
{
int n = 5;
int answer = countX(n);
cout << (answer);
}
|
Java
public class GFG {
static int countX(int n)
{
String binary = Integer.toBinaryString(n);
int count = 0;
for (int i = 0; i < binary.length(); i++) {
if (binary.charAt(i) == '1')
count++;
}
int answer = (int)Math.pow(2, count);
return answer;
}
public static void main(String args[])
{
int n = 5;
int answer = countX(n);
System.out.println(answer);
}
}
|
Python3
def countX(n):
binary = "{0:b}".format(n)
count = 0
for i in range(len(binary)):
if (binary[i] == '1'):
count += 1
answer = int(pow(2, count))
return answer
if __name__ == "__main__":
n = 5
answer = countX(n)
print(answer)
|
C#
using System;
class GFG
{
static int countX(int n)
{
string binary = Convert.ToString(n, 2);
int count = 0;
for (int i = 0; i < binary.Length; i++)
{
if (binary[i] == '1')
count++;
}
int answer = (int)Math.Pow(2, count);
return answer;
}
public static void Main()
{
int n = 5;
int answer = countX(n);
Console.WriteLine(answer);
}
}
|
Javascript
<script>
function countX(n)
{
let binary = (n >>> 0).toString(2);
let count = 0;
for(let i = 0; i < binary.length; i++)
{
if (binary[i] == '1')
count++;
}
let answer = Math.floor(Math.pow(2, count));
return answer;
}
let n = 5;
let answer = countX(n);
document.write(answer);
</script>
|
Time complexity: 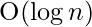
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...