Count of K length subsequence whose product is even
Last Updated :
05 May, 2021
Given an array arr[] and an integer K, the task is to find number of non empty subsequence of length K from the given array arr of size N such that the product of subsequence is a even number.
Example:
Input: arr[] = [2, 3, 1, 7], K = 3
Output: 3
Explanation:
There are 3 subsequences of length 3 whose product is even number {2, 3, 1}, {2, 3, 7}, {2, 1, 7}.
Input: arr[] = [2, 4], K = 1
Output: 2
Explanation:
There are 2 subsequence of length 1 whose product is even number {2} {4}.
Approach:
To solve the problem mentioned above we have to find the total number of subsequence of length K and subtract the count of K length subsequence whose product is odd.
- For making a product of the subsequence odd we must choose K numbers as odd.
- So the number of subsequences of length K whose product is odd is possibly finding k odd numbers, i.e., “o choose k” or
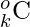
where o is the count of odd numbers in the subsequence. 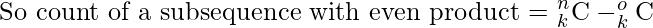
where n and o is the count of total numbers and odd numbers respectively.
Below is the implementation of above program:
C++
#include <bits/stdc++.h>
using namespace std;
int fact(int n);
int nCr(int n, int r)
{
if (r > n)
return 0;
return fact(n)
/ (fact(r)
* fact(n - r));
}
int fact(int n)
{
int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
int countSubsequences(
int arr[], int n, int k)
{
int countOdd = 0;
for (int i = 0; i < n; i++) {
if (arr[i] & 1)
countOdd++;
}
int ans = nCr(n, k)
- nCr(countOdd, k);
return ans;
}
int main()
{
int arr[] = { 2, 4 };
int K = 1;
int N = sizeof(arr) / sizeof(arr[0]);
cout << countSubsequences(arr, N, K);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int nCr(int n, int r)
{
if (r > n)
return 0;
return fact(n) / (fact(r) *
fact(n - r));
}
static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int countSubsequences(int arr[],
int n, int k)
{
int countOdd = 0;
for(int i = 0; i < n; i++)
{
if (arr[i] % 2 == 1)
countOdd++;
}
int ans = nCr(n, k) - nCr(countOdd, k);
return ans;
}
public static void main(String args[])
{
int arr[] = { 2, 4 };
int K = 1;
int N = arr.length;
System.out.println(countSubsequences(arr, N, K));
}
}
|
Python3
def nCr(n, r):
if (r > n):
return 0
return fact(n) // (fact(r) *
fact(n - r))
def fact(n):
res = 1
for i in range(2, n + 1):
res = res * i
return res
def countSubsequences(arr, n, k):
countOdd = 0
for i in range(n):
if (arr[i] & 1):
countOdd += 1;
ans = nCr(n, k) - nCr(countOdd, k);
return ans
arr = [ 2, 4 ]
K = 1
N = len(arr)
print(countSubsequences(arr, N, K))
|
C#
using System;
class GFG{
static int nCr(int n, int r)
{
if (r > n)
return 0;
return fact(n) / (fact(r) *
fact(n - r));
}
static int fact(int n)
{
int res = 1;
for(int i = 2; i <= n; i++)
res = res * i;
return res;
}
static int countSubsequences(int []arr,
int n, int k)
{
int countOdd = 0;
for(int i = 0; i < n; i++)
{
if (arr[i] % 2 == 1)
countOdd++;
}
int ans = nCr(n, k) - nCr(countOdd, k);
return ans;
}
public static void Main(String []args)
{
int []arr = { 2, 4 };
int K = 1;
int N = arr.Length;
Console.WriteLine(countSubsequences(arr, N, K));
}
}
|
Javascript
<script>
function nCr(n, r)
{
if (r > n)
return 0;
return fact(n)
/ (fact(r)
* fact(n - r));
}
function fact(n)
{
var res = 1;
for (var i = 2; i <= n; i++)
res = res * i;
return res;
}
function countSubsequences( arr, n, k)
{
var countOdd = 0;
for (var i = 0; i < n; i++) {
if (arr[i] & 1)
countOdd++;
}
var ans = nCr(n, k)
- nCr(countOdd, k);
return ans;
}
var arr = [ 2, 4 ];
var K = 1;
var N = arr.length;
document.write( countSubsequences(arr, N, K));
</script>
|
Share your thoughts in the comments
Please Login to comment...