Count of groups among N people having only one leader in each group

Given N number of people, the task is to count the number of ways to form groups of size? N where, in each group, the first element of the group is the leader of the group.
Note:

• Groups with same people having different leaders are treated as a different group. For Example: The group {1, 2, 3} and {2, 1, 3} are treated as different group as they have different leader 1 and 2 respectively.
• Groups with same leader having same people are treated as a same group. For Example: The groups {1, 3, 2} and {1, 2, 3} are treated as same group as they have same leader and same people.
• The answer can be very large, take modulo to (1e9+7).

Examples:

Input: N = 3 
Output: 12 
Explanation:
Total Groups with leaders are: 
Groups with Leader 1: 
1. {1} 
2. {1, 2} 
3. {1, 3} 
4. {1, 2, 3} 
Groups with Leader 2: 
5. {2} 
6. {2, 1} 
7. {2, 3} 
8. {2, 1, 3} 
Groups with Leader 3: 
9. {3} 
10. {3, 1} 
11. {3, 2} 
12. {3, 1, 2}
Input: N = 5 
Output: 80

Approach: This problem can be solved using the concept of Binomial coefficients and modular exponentiation. Below are the observations to this problem statement:

• The number of ways to select one leader among N persons is C(N, 1).
• For every leader we can select a group of size K where 0 ? K ? N-1 to make the possible number of grouping.
• So the total number ways is given by the product of N and the summation of selection K elements from the remaining (N – 1) elements as:

Total Ways =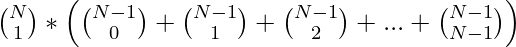 

By using Binomial Theorem, the summation of the Binomial Coefficient can be written as:

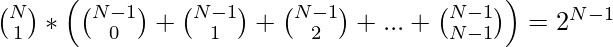
Therefore the number of ways of selecting groups having only one leader is

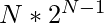
Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

long long mod = 1000000007;

// Function to find 2^x using
// modular exponentiation
int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;

    // If B is even
    long long y;
    if (B % 2 == 0) {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }

    // If B is odd
    else {
        y = A % mod;
        y = (y * exponentMod(A, B - 1)
             % mod)
            % mod;
    }

    return (int)((y + mod) % mod);
}

// Function to count the number of
// ways to form the group having
// one leader
void countWays(int N)
{

    // Find 2^(N-1) using modular
    // exponentiation
    long long select = exponentMod(2,
                                   N - 1);

    // Count total ways
    long long ways
        = ((N % mod)
           * (select % mod));

    ways %= mod;

    // Print the total ways
    cout << ways;
}

// Driver Code
int main()
{

    // Given N number of peoples
    int N = 5;

    // Function Call
    countWays(N);
}

Java

// Java program for the above approach
import java.util.*;
class GFG{

static long mod = 1000000007;

// Function to find 2^x using
// modular exponentiation
static int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;

    // If B is even
    long y;
    if (B % 2 == 0)
    {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }

    // If B is odd
    else
    {
        y = A % mod;
        y = (y * exponentMod(A, B - 1) %
                                  mod) % mod;
    }

    return (int)((y + mod) % mod);
}

// Function to count the number of
// ways to form the group having
// one leader
static void countWays(int N)
{

    // Find 2^(N-1) using modular
    // exponentiation
    long select = exponentMod(2, N - 1);

    // Count total ways
    long ways = ((N % mod) * (select % mod));

    ways %= mod;

    // Print the total ways
    System.out.print(ways);
}

// Driver Code
public static void main(String[] args)
{

    // Given N number of peoples
    int N = 5;

    // Function Call
    countWays(N);
}
}

// This code is contributed by sapnasingh4991

Python3

# Python3 program for the above approach
mod = 1000000007

# Function to find 2^x using
# modular exponentiation
def exponentMod(A, B):

    # Base cases
    if (A == 0):
        return 0;
    if (B == 0):
        return 1;

    # If B is even
    y = 0;

    if (B % 2 == 0):
        y = exponentMod(A, B // 2);
        y = (y * y) % mod;

    # If B is odd
    else:
        y = A % mod;
        y = (y * exponentMod(A, B - 1) %
                                  mod) % mod;

    return ((y + mod) % mod);

# Function to count the number of
# ways to form the group having
# one leader
def countWays(N):

    # Find 2^(N-1) using modular
    # exponentiation
    select = exponentMod(2, N - 1);

    # Count total ways
    ways = ((N % mod) * (select % mod));

    ways %= mod;

    # Print the total ways
    print(ways)

# Driver code
if __name__=='__main__':

    # Given N number of people
    N = 5;

    # Function call
    countWays(N);

# This code is contributed by rutvik_56

C#

// C# program for the above approach
using System;
class GFG{

static long mod = 1000000007;

// Function to find 2^x using
// modular exponentiation
static int exponentMod(int A, int B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;

    // If B is even
    long y;
    if (B % 2 == 0)
    {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }

    // If B is odd
    else
    {
        y = A % mod;
        y = (y * exponentMod(A, B - 1) %
                                  mod) % mod;
    }

    return (int)((y + mod) % mod);
}

// Function to count the number of
// ways to form the group having
// one leader
static void countWays(int N)
{

    // Find 2^(N-1) using modular
    // exponentiation
    long select = exponentMod(2, N - 1);

    // Count total ways
    long ways = ((N % mod) * (select % mod));

    ways %= mod;

    // Print the total ways
    Console.Write(ways);
}

// Driver Code
public static void Main(String[] args)
{

    // Given N number of peoples
    int N = 5;

    // Function Call
    countWays(N);
}
}

// This code is contributed by sapnasingh4991

Javascript

<script>

// Javascript program for the above approach

let mod = 1000000007;

// Function to find 2^x using
// modular exponentiation
function exponentMod(A, B)
{
    // Base cases
    if (A == 0)
        return 0;
    if (B == 0)
        return 1;

    // If B is even
    let y;
    if (B % 2 == 0) {
        y = exponentMod(A, B / 2);
        y = (y * y) % mod;
    }

    // If B is odd
    else {
        y = A % mod;
        y = (y * exponentMod(A, B - 1)
            % mod)
            % mod;
    }

    return ((y + mod) % mod);
}

// Function to count the number of
// ways to form the group having
// one leader
function countWays(N)
{

    // Find 2^(N-1) using modular
    // exponentiation
    let select = exponentMod(2,
                                N - 1);

    // Count total ways
    let ways
        = ((N % mod)
        * (select % mod));

    ways %= mod;

    // Print the total ways
    document.write(ways);
}

// Driver Code

    // Given N number of peoples
    let N = 5;

    // Function Call
    countWays(N);

// This code is contributed by Mayank Tyagi

</script>

Output:

80

Time Complexity: O(log N) 
Auxiliary Space: O(N)