Count of decreasing pairs formed from numbers 1 to N
Last Updated :
22 Feb, 2023
Given an integer N, the task is to count of decreasing pairs from numbers 1 to N.
A pair (x, y) is said to be decreasing if x > y
Examples:
Input: N = 8
Output: 3
Explanation:
Decreasing pairs are: (7, 1), (6, 2), (5, 3).
Input: N = 9
Output: 4
Explanation:
Decreasing pairs are: (8, 1), (7, 2), (6, 3), (5, 4).
Approach: Consider the below cases:
If N = 1 => Count = 0
If N = 2 => Count = 1 {(2, 1)}
If N = 3 => Count = 1 {(3, 1) or (3, 2)}
If N = 4 => Count = 2 {(4, 3), (2, 1)}
If N = 5 => Count = 2 {(5, 4), (3, 2)}
If N = 6 => Count = 3 {(6, 5), (4, 3), (2, 1)}
.
.
and so on
It can be clearly observed that
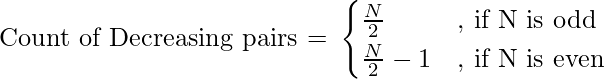
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int divParts(int N)
{
if (N % 2 == 0)
cout << (N / 2) - 1 << endl;
else
cout << N / 2 << endl;
}
int main()
{
int N = 8;
divParts(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static void divParts(int N)
{
if (N % 2 == 0)
System.out.println((N / 2) - 1);
else
System.out.println((N / 2));
}
public static void main(String[] args)
{
int N = 8;
divParts(N);
}
}
|
Python3
def divParts(N):
if (N % 2 == 0):
print((N / 2) - 1);
else:
print(N / 2);
N = 8;
divParts(N);
|
C#
using System;
class GFG{
static void divParts(int N)
{
if (N % 2 == 0)
Console.WriteLine((N / 2) - 1);
else
Console.WriteLine((N / 2));
}
public static void Main()
{
int N = 8;
divParts(N);
}
}
|
Javascript
<script>
function divParts(N)
{
if (N % 2 == 0)
document.write((N / 2) - 1);
else
document.write((N / 2));
}
let N = 8;
divParts(N);
</script>
|
Time Complexity: O(1)
Space Complexity: O(1) as no extra space has been used.
Share your thoughts in the comments
Please Login to comment...