Count inversions in an array | Set 4 ( Using Trie )
Last Updated :
22 Jun, 2021
Inversion Count for an array indicates – how far (or close) the array is from being sorted. If the array is already sorted then inversion count is 0. If the array is sorted in reverse order that inversion count is the maximum.
Two elements a[i] and a[j] form an inversion if a[i] > a[j] and i < j.
For simplicity, we may assume that all elements are unique.
So, our task is to count the number of inversions in the array. That is the number of pair of elements (a[i], a[j]) such that:
Example:
Input: arr[] = {8, 4, 2, 1}
Output: 6
Given array has six inversions (8, 4), (4, 2),
(8, 2), (8, 1), (4, 1), (2, 1).
Input: arr[] = { 1, 20, 6, 4, 5 }
Output: 5
- Naive and Modified Merge Sort
- Using AVL Tree
- Using BIT
Approach:
We will iterate backwards in the array and store each element into the Trie. To store a number in Trie we
have to break the number into its binary form and If the bit is 0 then it signifies we store that bit into the left pointer of the current node and if it is 1 we will store it into the right pointer of the current node and correspondingly change the current node. We will also maintain the count which signifies how many numbers follow the same path till that node.
Structure of Node of the Trie
struct node{
int count;
node* left;
node* right;
};
At any point, while we are storing the bits, we happen to move to the right pointer (i.e the bit is 1) we will check if the left child exists then this means there are numbers which are smaller than the current number who are already been stored into the Trie, these numbers are only the inversion count so we will add these to the count.
Below is the implementation of the approach
C++
#include <iostream>
using namespace std;
struct Node {
int count;
Node* left;
Node* right;
};
Node* makeNewNode()
{
Node* temp = new Node;
temp->count = 1;
temp->left = NULL;
temp->right = NULL;
return temp;
}
void insertElement(int num,
Node* root,
int& ans)
{
for (int i = 63; i >= 0; i--) {
int a = (num & (1 << i));
if (a != 0) {
if (root->left != NULL)
ans += root->left->count;
if (root->right != NULL) {
root = root->right;
root->count += 1;
}
else {
Node* temp = makeNewNode();
root->right = temp;
root = root->right;
}
}
else {
if (root->left != NULL) {
root = root->left;
root->count++;
}
else {
Node* temp = makeNewNode();
root->left = temp;
root = root->left;
}
}
}
}
int getInvCount(int arr[], int n)
{
Node* head = makeNewNode();
int ans = 0;
for (int i = n - 1; i >= 0; i--) {
insertElement(arr[i],
head,
ans);
}
return ans;
}
int main()
{
int arr[] = { 8, 4, 2, 1 };
int n = sizeof(arr) / sizeof(int);
cout << "Number of inversions are : "
<< getInvCount(arr, n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class Node
{
int count;
Node left;
Node right;
};
static int ans;
static Node makeNewNode()
{
Node temp = new Node();
temp.count = 1;
temp.left = null;
temp.right = null;
return temp;
}
static void insertElement(int num,
Node root)
{
for (int i = 63; i >= 0; i--)
{
int a = (num & (1 << i));
if (a != 0)
{
if (root.left != null)
ans += root.left.count;
if (root.right != null)
{
root = root.right;
root.count += 1;
}
else
{
Node temp = makeNewNode();
root.right = temp;
root = root.right;
}
}
else
{
if (root.left != null)
{
root = root.left;
root.count++;
}
else
{
Node temp = makeNewNode();
root.left = temp;
root = root.left;
}
}
}
}
static int getInvCount(int arr[], int n)
{
Node head = makeNewNode();
ans = 0;
for (int i = n - 1; i >= 0; i--)
{
insertElement(arr[i],
head);
}
return ans;
}
public static void main(String[] args)
{
int arr[] = { 8, 4, 2, 1 };
int n = arr.length;
System.out.print("Number of inversions are : "
+ getInvCount(arr, n));
}
}
|
Python3
class Node:
def __init__(self):
self.left = self.right = None
self.count = 1
def makeNewNode():
temp = Node()
return temp
def insertElement(num, root, ans):
for i in range(63, -1, -1):
a = (num & (1 << i));
if (a != 0):
if (root.left != None):
ans += root.left.count;
if (root.right != None):
root = root.right;
root.count += 1;
else:
temp = makeNewNode();
root.right = temp;
root = root.right;
else:
if (root.left != None):
root = root.left;
root.count += 1
else:
temp = makeNewNode();
root.left = temp;
root = root.left;
return ans
def getInvCount(arr, n):
head = makeNewNode();
ans = 0;
for i in range(n - 1 ,-1, -1):
ans = insertElement(arr[i], head, ans);
return ans;
if __name__=='__main__':
arr = [ 8, 4, 2, 1 ]
n = len(arr)
print("Number of inversions are : " + str(getInvCount(arr, n)))
|
C#
using System;
class GFG
{
public class Node
{
public int count;
public Node left;
public Node right;
};
static int ans;
static Node makeNewNode()
{
Node temp = new Node();
temp.count = 1;
temp.left = null;
temp.right = null;
return temp;
}
static void insertElement(int num,
Node root)
{
for (int i = 63; i >= 0; i--)
{
int a = (num & (1 << i));
if (a != 0)
{
if (root.left != null)
ans += root.left.count;
if (root.right != null)
{
root = root.right;
root.count += 1;
}
else
{
Node temp = makeNewNode();
root.right = temp;
root = root.right;
}
}
else
{
if (root.left != null)
{
root = root.left;
root.count++;
}
else
{
Node temp = makeNewNode();
root.left = temp;
root = root.left;
}
}
}
}
static int getInvCount(int []arr, int n)
{
Node head = makeNewNode();
ans = 0;
for (int i = n - 1; i >= 0; i--)
{
insertElement(arr[i], head);
}
return ans;
}
public static void Main(String[] args)
{
int []arr = { 8, 4, 2, 1 };
int n = arr.Length;
Console.Write("Number of inversions are : " +
getInvCount(arr, n));
}
}
|
Javascript
<script>
class Node
{
constructor()
{
this.count = 0;
this.left = null;
this.right = null;
}
};
var ans = 0;
function makeNewNode()
{
var temp = new Node();
temp.count = 1;
temp.left = null;
temp.right = null;
return temp;
}
function insertElement(num, root)
{
for (var i = 63; i >= 0; i--)
{
var a = (num & (1 << i));
if (a != 0)
{
if (root.left != null)
ans += root.left.count;
if (root.right != null)
{
root = root.right;
root.count += 1;
}
else
{
var temp = makeNewNode();
root.right = temp;
root = root.right;
}
}
else
{
if (root.left != null)
{
root = root.left;
root.count++;
}
else
{
var temp = makeNewNode();
root.left = temp;
root = root.left;
}
}
}
}
function getInvCount(arr, n)
{
var head = makeNewNode();
ans = 0;
for (var i = n - 1; i >= 0; i--)
{
insertElement(arr[i], head);
}
return ans;
}
var arr = [8, 4, 2, 1];
var n = arr.length;
document.write("Number of inversions are : " +
getInvCount(arr, n));
</script>
|
Output: Number of inversions are : 6
Time Complexity: 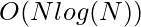
Auxiliary Space: 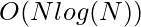
Share your thoughts in the comments
Please Login to comment...