Count inversions of size k in a given array
Last Updated :
02 Jan, 2023
Given an array of n distinct integers 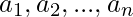 and an integer k. Find out the number of sub-sequences of a such that
and an integer k. Find out the number of sub-sequences of a such that  , and
, and 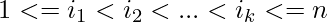 . In other words output the total number of inversions of length k. Examples:
. In other words output the total number of inversions of length k. Examples:
Input : a[] = {9, 3, 6, 2, 1}, k = 3
Output : 7
The seven inversions are {9, 3, 2}, {9, 3, 1},
{9, 6, 2}, {9, 6, 1}, {9, 2, 1}, {3, 2, 1} and
{6, 2, 1}.
Input : a[] = {5, 6, 4, 9, 2, 7, 1}, k = 4
Output : 2
The two inversions are {5, 4, 2, 1}, {6, 4, 2, 1}.
We have already discussed counting inversion of length three here. This post will generalise the approach using Binary Indexed Tree and Counting inversions using BIT. More on Binary Indexed Trees can be found from the actual paper that Peter M. Fenwick published, here. 1. To begin with, we first convert the given array to a permutation of elements 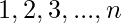 (Note that this is always possible since the elements are distinct). 2. The approach is to maintain a set of k Fenwick Trees. Let it be denoted by
(Note that this is always possible since the elements are distinct). 2. The approach is to maintain a set of k Fenwick Trees. Let it be denoted by ![Rendered by QuickLaTeX.com bit[k][n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e90d75d930f6ef5e0856c1e6e66a9d0_l3.png) where
where ![Rendered by QuickLaTeX.com bit[l][x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc1016ecc3c8f61b0081eec43eac60b9_l3.png) , keeps track of the number of
, keeps track of the number of 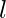 – length sub-sequences that start with
– length sub-sequences that start with 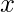 . 3. We iterate from the end of the converted array to the beginning. For every converted array element
. 3. We iterate from the end of the converted array to the beginning. For every converted array element 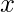 , we update the Fenwick tree set, as: For each
, we update the Fenwick tree set, as: For each 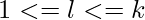 , each sub-sequence of length
, each sub-sequence of length 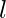 that start with a number less than
that start with a number less than 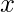 is also a part of sequences of length
is also a part of sequences of length 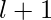 . The final result is found by sum of occurrences of
. The final result is found by sum of occurrences of 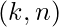 . The implementation is discussed below:
. The implementation is discussed below:
C++
#include <bits/stdc++.h>
using namespace std;
const int K = 51;
const int N = 100005;
int BIT[K][N] = { 0 };
void updateBIT(int t, int i, int val, int n)
{
while (i <= n) {
BIT[t][i] = BIT[t][i] + val;
i = i + (i & (-i));
}
}
int getSum(int t, int i)
{
int res = 0;
while (i > 0) {
res = res + BIT[t][i];
i = i - (i & (-i));
}
return res;
}
void convert(int arr[], int n)
{
int temp[n];
for (int i = 0; i < n; i++)
temp[i] = arr[i];
sort(temp, temp + n);
for (int i = 0; i < n; i++) {
arr[i] = lower_bound(temp, temp + n,
arr[i]) - temp + 1;
}
}
int getInvCount(int arr[], int n, int k)
{
convert(arr, n);
for (int i = n - 1; i >= 0; i--) {
int x = arr[i];
updateBIT(1, x, 1, n);
for (int l = 1; l < k; l++) {
updateBIT(l + 1, x, getSum(l, x - 1), n);
}
}
return getSum(k, n);
}
int main()
{
int arr[] = { 5, 6, 4, 9, 3, 7, 2, 1 };
int n = sizeof(arr) / sizeof(arr[0]);
int k = 4;
cout << "Inversion Count : " << getInvCount(arr, n, k);
return 0;
}
|
Java
import java.io.*;
import java.util.Arrays;
import java.util.ArrayList;
import java.lang.*;
import java.util.Collections;
class GFG
{
static int K = 51;
static int N = 100005;
static int BIT[][] = new int[K][N];
static void updateBIT(int t, int i,
int val, int n)
{
while (i <= n)
{
BIT[t][i] = BIT[t][i] + val;
i = i + (i & (-i));
}
}
static int getSum(int t, int i)
{
int res = 0;
while (i > 0)
{
res = res + BIT[t][i];
i = i - (i & (-i));
}
return res;
}
static void convert(int arr[], int n)
{
int temp[] = new int[n];
for (int i = 0; i < n; i++)
temp[i] = arr[i];
Arrays.sort(temp);
for (int i = 0; i < n; i++)
{
arr[i] = Arrays.binarySearch(temp,
arr[i]) + 1;
}
}
static int getInvCount(int arr[],
int n, int k)
{
convert(arr, n);
for (int i = n - 1; i >= 0; i--)
{
int x = arr[i];
updateBIT(1, x, 1, n);
for (int l = 1; l < k; l++)
{
updateBIT(l + 1, x,
getSum(l, x - 1), n);
}
}
return getSum(k, n);
}
public static void main(String[] args)
{
int arr[] = { 5, 6, 4, 9,
3, 7, 2, 1 };
int n = arr.length;
int k = 4;
System.out.println("Inversion Count : " +
getInvCount(arr, n, k));
}
}
|
Python3
K = 51
N = 100005
BIT = [[0 for x in range(N)]
for y in range(K)]
def updateBIT(t, i, val, n):
while (i <= n):
BIT[t][i] = BIT[t][i] + val
i = i + (i & (-i))
def getSum(t, i):
res = 0
while (i > 0):
res = res + BIT[t][i]
i = i - (i & (-i))
return res
def convert( arr, n):
temp = [0] * n
for i in range(n):
temp[i] = arr[i]
temp = sorted(temp)
j = 1
for i in temp:
arr[arr.index(i)] = j
j += 1
def getInvCount(arr, n, k) :
convert(arr, n)
for i in range(n - 1, -1, -1):
x = arr[i]
updateBIT(1, x, 1, n)
for l in range(1, k):
updateBIT(l + 1, x, getSum(l, x - 1), n)
return getSum(k, n)
if __name__ =="__main__":
arr = [5, 6, 4, 9, 3, 7, 2, 1]
n = 8
k = 4
print("Inversion Count :",
getInvCount(arr, n, k))
|
C#
using System;
using System.Linq;
class GFG
{
static int K = 51;
static int N = 100005;
static int [,]BIT = new int[K, N];
static void updateBIT(int t, int i,
int val, int n)
{
while (i <= n)
{
BIT[t, i] = BIT[t, i] + val;
i = i + (i & (-i));
}
}
static int getSum(int t, int i)
{
int res = 0;
while (i > 0)
{
res = res + BIT[t, i];
i = i - (i & (-i));
}
return res;
}
static void convert(int []arr, int n)
{
int []temp = new int[n];
for (int i = 0; i < n; i++)
temp[i] = arr[i];
Array.Sort(temp);
for (int i = 0; i < n; i++)
{
arr[i] = Array.BinarySearch(temp,
arr[i]) + 1;
}
}
static int getInvCount(int []arr,
int n, int k)
{
convert(arr, n);
for (int i = n - 1; i >= 0; i--)
{
int x = arr[i];
updateBIT(1, x, 1, n);
for (int l = 1; l < k; l++)
{
updateBIT(l + 1, x,
getSum(l, x - 1), n);
}
}
return getSum(k, n);
}
public static void Main(String[] args)
{
int []arr = { 5, 6, 4, 9,
3, 7, 2, 1 };
int n = arr.Length;
int k = 4;
Console.WriteLine("Inversion Count : " +
getInvCount(arr, n, k));
}
}
|
Javascript
let K = 51;
let N = 100005;
let BIT = new Array(K).fill(0).map(() => new Array(N).fill(0));
function updateBIT(t, i, val, n)
{
while (i <= n) {
BIT[t][i] = BIT[t][i] + val;
i = i + (i & (-i));
}
}
function getSum(t, i)
{
let res = 0;
while (i > 0) {
res = res + BIT[t][i];
i = i - (i & (-i));
}
return res;
}
function convert(arr, n)
{
let temp=new Array(n);
for (let i = 0; i < n; i++)
temp[i] = arr[i];
temp.sort();
for (let i = 0; i < n; i++) {
arr[i] = lower_bound(temp, 0, n, arr[i])+1;
}
}
function lower_bound(a, low, high, element)
{
while(low < high)
{
let middle = low + parseInt((high - low) / 2, 10);
if(element > a[middle])
low = middle + 1;
else
high = middle;
}
return low;
}
function getInvCount(arr, n, k)
{
convert(arr, n);
for (let i = n - 1; i >= 0; i--) {
let x = arr[i];
updateBIT(1, x, 1, n);
for (let l = 1; l < k; l++) {
updateBIT(l + 1, x, getSum(l, x - 1), n);
}
}
return getSum(k, n);
}
let arr = [ 5, 6, 4, 9, 3, 7, 2, 1 ];
let n = arr.length;
let k = 4;
console.log("Inversion Count : " + getInvCount(arr, n, k));
|
Output:
Inversion Count : 11
Time Complexity 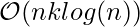 Auxiliary Space
Auxiliary Space 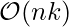 It should be noted that this is not the only approach to solve the problem of finding k-inversions. Obviously, any problem solvable by BIT is also solvable by Segment Tree. Besides, we can use Merge-Sort based algorithm, and C++ policy based data structure too. Also, at the expense of higher time complexity, Dynamic Programming approach can also be used.
It should be noted that this is not the only approach to solve the problem of finding k-inversions. Obviously, any problem solvable by BIT is also solvable by Segment Tree. Besides, we can use Merge-Sort based algorithm, and C++ policy based data structure too. Also, at the expense of higher time complexity, Dynamic Programming approach can also be used.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...