Corollaries of Binomial Theorem

Last Updated : 02 Jun, 2018

The expression 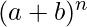$(a+b)^n$ denotes 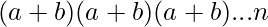$(a+b)(a+b)(a+b) ... n$ times.
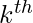This can be evaluated as the sum of the terms involving $a^k b^{n-k}$ for k = 0 to n, where the first term can be chosen from n places, second term from (n-1) places, $k^{th}$ term from (n-(k-1)) places and so on. This is expressed as $(a+b)^n = \sum\limits_{k=0}^n ^nC_k a^{n-k} b^k$ .
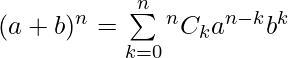The binomial expansion using Combinatorial symbols is

$(a+b)^n = ^nC_0 a^n b^0 + ^nC_1 a^{n-1} b^1 + ^nC_2 a^{n-2} b^2 .. + ^nC_{n-k} a^k b^{n-k} .. +^nC_n a^0 b^n$

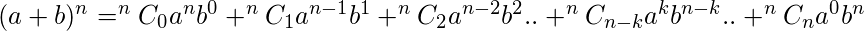
The degree of each term 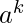$a^k$ $b^{n-k}$ in the above binomial expansion is of the order n.
The number of terms in the expansion is n+1.
$^nC_k = n!/k!(n-k)!$
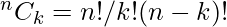Similarly $^nC_{n-k} = n!/(n-k)!(n-(n-k))! = n!/(n-k)!k!$
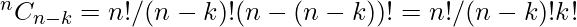Hence it can be concluded that $^nC_k = ^nC_{n-k}$ .

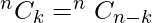Substituting a = 1 and b = x in the binomial expansion, for any positive integer n we obtain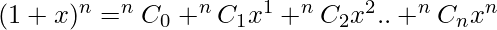
$(1+x)^n = ^nC_0 + ^nC_1 x^1 + ^nC_2 x^2 ..+ ^nC_n x^n$ .

Corollary 1:

$\sum\limits_{k=0}^n ^nC_k = 2^n$

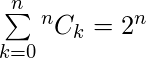
for any non-negative integer n.

Replacing x with 1 in the above binomial expansion, We obtain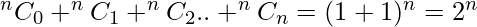
$^nC_0 + ^nC_1 + ^nC_2 .. + ^nC_n = (1+1)^n = 2^n$ .

Corollary 2:

$\sum\limits_{k=0}^n ^nC_k = 0$

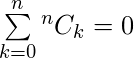
for any positive integer n.

Replacing x with -1 in the above binomial expansion, We obtain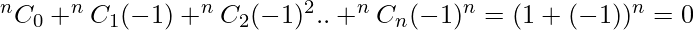
$^nC_0 + ^nC_1 (-1) + ^nC_2 (-1)^2 .. + ^nC_n (-1)^n = (1+(-1))^n = 0$ .

Corollary 3:

Replacing x with 2 in the above binomial expansion, we obtain
$^nC_0 + ^nC_1 2 + ^nC_2 2^2 .. + ^nC_n 2^n = (1+2)^n = 3^n$

In general, it can be said that

$\sum\limits_{k=0}^n (2^k) ^nC_k = 3^n$

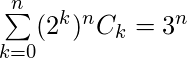
Additionally, one can combine corollary 1 and corollary 2 to get another result,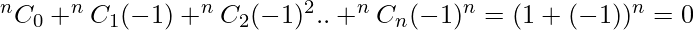

$^nC_0 + ^nC_1 (-1) + ^nC_2 (-1)^2 .. + ^nC_n (-1)^n = (1+(-1))^n = 0$

$^nC_0 + ^nC_2 + .. = ^nC_1 + ^nC_3 + ...$
Sum of coefficients of even terms = Sum of coefficients of odd terms.

Since $\sum\limits_{k=0}^n ^nC_k = 2^n$ ,

2( $^nC_0 + ^nC_2 + ..) = 2^n$

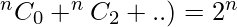$^nC_0 + ^nC_2 + .. = 2^{n-1}$

$^nC_0 + ^nC_2 + .. = ^nC_1 + ^nC_3 + .. = 2^{n-1}$

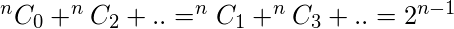
Counting
The coefiecients of the terms in the expansion 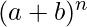$(a+b)^n$ correspond to the terms of the pascal’s triangle in row n.

$(a+b)^0$	1	1
$(a+b)^1$	$a+b$	$1 \ 1$
$(a+b)^2$	$a^2+2ab+b^2$	$1 \ 2 \ 1$
$(a+b)^3$	$a^3+3a^2b+3ab^2+b^3$	$1 \ 3 \ 3 \ 1$

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live

My Personal Notes

Related Articles