Chords of a Circle

Chord of a circle is the line that joints any two points on the circumference of the circle. A circle can have various chords and the largest chord of a circle is the diameter of the circle. We can easily calculate the length of the chord using the Chord Length Formula. As the name suggests it is the formula for calculating the length of the chord in a circle in Geometry.

In this article, we will learn about the definition of the chord, theorems of the chords and the circle, explain its properties, and the formulas to calculate the length of the chord using different methods. The article also has some solved sample problems for better understanding.

Circle Definition

A circle is a perfect round shape consisting of all points in a plane that are placed at a given distance from a given point. They consist of a closed curved line around a central point. The points present on the line are at the same distance from the central point. The distance to the centre of a circle is called a radius.

Chord of a Circle Definition

The line segment that joins any two points on the circumference of the circle is known as the chord of a circle. As the diameter also joins the two points on the circumference of a circle, thus it is also a chord to a circle. In fact, the diameter is the longest chord to the circle. In other words, the chord is a line segment whose both ends lie on the circumference of a circle. The following illustration can help us understand more.

What is Chord Length Formula?

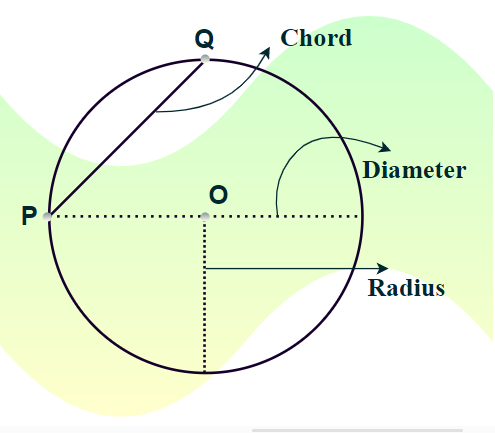
There are two basic methods or formulas to calculate the length of the chord. a chord length can be determined by using the perpendicular distance from the centre of the circle as well as by the trigonometric method. Thus the length of a chord can be found

• Using the Pythagorean Theorem
• Using the Law of Cosines

Let’s understand these methods in detail as follows:

Method 1: Using the Pythagorean Theorem

In the following diagram for a chord, as we know the perpendicular drawn from the centre of the circle to the chord bisects it in two halves.

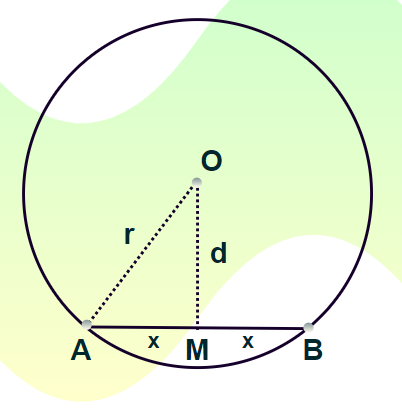
In triangles OAM, using Pythagoras Theorem,

r² = x² + d²

⇒ x² = r² – d²

⇒ x = √(r² – d²)

As x is half the length of the chord,

Thus, the chord length for any circle with its perpendicular distance from the centre is known is given as

Length of a Chord of a Circle = 2 ×[√(r² – d²)]

Where,

• r is the radius of circle, and 
• d is the perpendicular distance between center of circle and chord.

Method 2: Using the Law of Cosines

As we know for a triangle ABC, with sides a, b and c, the Law of cosine states,

c² = a² + b² – 2ab cos C

Using, this law in the following diagram of a chord subtending θ angle at the centre of the circle, we can find the length of the chord.

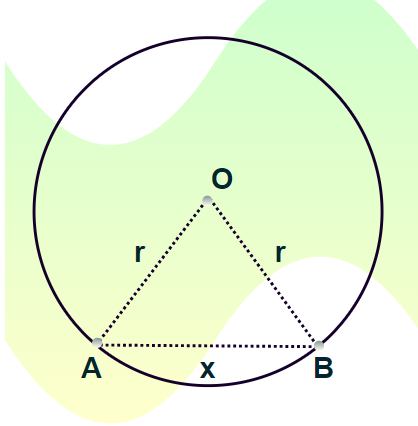
In triangle OAB, using the Law of cosine,

⇒ x² = r² + r² – 2×r×r×cos θ

⇒ x² = 2r²– 2r²cos θ

⇒ x² = 2r²(1- cos θ)

⇒ x =[Tex] \sqrt{2r^2(1- \cos \theta)} [/Tex]

[Tex] \Rightarrow x =r\sqrt{2(\sin^2 \theta/2 + \cos^2 \theta/2 – \cos^2 \theta/2 + \sin^2 \theta/2)} [/Tex]

[Tex] \Rightarrow x =r\sqrt{4\sin^2 \theta/2 } [/Tex]

[Tex] \Rightarrow x =2r\sin \theta/2 [/Tex]

Thus, the Chord length is given by:

Chord Length = 2r × sin [θ/2]

Where, 

• θ is the angle subtended by the chord at the center, and 
• r is the radius of the circle.

Other Related Formula for Chord Length

When two circles share a common chord, then the length of that common chord can be calculated using the formula

Length of a Common Chord of Two Circles = 2R₁ × R₂ / D

Where,

• R₁ and R₂ refers to radius of circles
• D is the distance between the two centers of the circle

Chord of a Circle Theorems

The chord of the circle subtends the angle at the centre of the circle which helps us to prove various concepts in the circle. There are various theorems based on the chord of a circle,

• Theorem 1: Equal Chords Equal Angles Theorem
• Theorem 2: Equal Angles Equal Chords Theorem (Converse of Theorem 1)
• Theorem 3: Equal Chords Equidistant from Center Theorem

Now, let’s discuss the same in the article below.

Theorem 1: Equal Chords Equal Angles Theorem

Statements: Equal chords subtends equal angles at the centre of the circle, i.e. the angle subtends by the chord are equal if the chord is equal.

Proof:

From the figure,

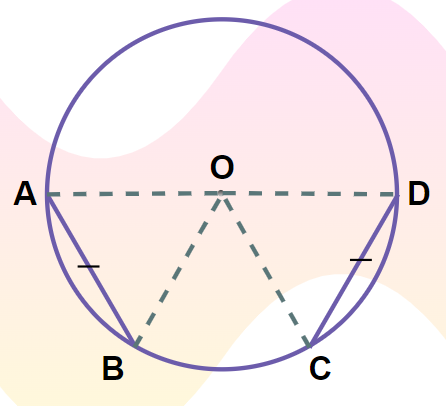
In ∆AOB and ∆DOC

• AB = CD …eq(i) (Given)
• OA = OD …eq(ii) (Radius of Circle)
• OB = OC …eq(iii) (Radius of Circle)

Thus, by SSS congruency conditions the Triangle ∆AOB and ∆COD are congruent.

Thus,

∠AOB = ∠DOC (By CPCT)

Thus, the theorem is verified.

Theorem 2: Equal Angles Equal Chords Theorem (Converse of Theorem 1)

Statement: Chords subtending equal angles at the centre of a circle are equal in length. This is the converse of the first theorem.

From the figure,

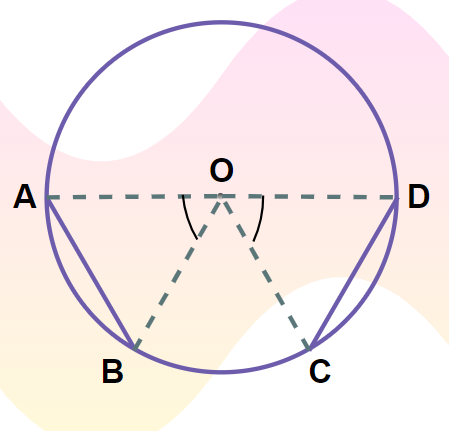
In ∆AOB and ∆DOC

• ∠AOB = ∠DOC …eq(i) (Given)
• OA = OD …eq(ii) (Radius of Circle)
• OB = OC …eq(iii) (Radius of Circle)

Thus, by SAS congruency conditions the Triangle ∆AOB and ∆COD are congruent.

Thus,

AB = CD (By CPCT)

Thus, the theorem is verified.

Theorem 3: Equal Chords Equidistant from Center Theorem

Statement: Equal chords are equidistant from the centre, i.e. the distance between the centre of the circle and the equal chord is always equal.

From the figure,

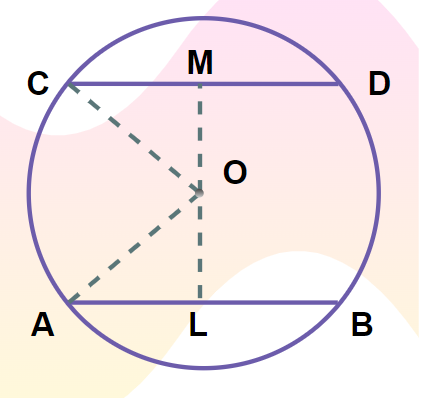
In ∆AOL and ∆COM

• ∠ALO = ∠CMO …eq(i) (90 degrees)
• OA = OC …eq(ii) (Radius of Circle)
• OL = OM …eq(iii) (Given)

Thus, by RHS congruency conditions the Triangle ∆AOB and ∆COD are congruent.

Thus,

AL = CM (By CPCT)…(iv)

Now, we know that the perpendicular drawn from the centre bisects the chords.

From eq(iv)

2AL = 2CM

AB = CD

Thus, the theorem is verified.

Properties of Chords of a Circle

There are various properties of chords in a circle, some of those properties are as follows:

• A chord that passes through the centre of a circle is called a diameter, and it is the longest chord in the circle.
• The perpendicular to a chord, that is drawn from the centre of the circle bisects the chord.
• Chords that are equidistant from the centre of a circle are equal in length.
• There is only one circle that passes through three collinear points.
• Chords that are equal in length subtend equal angles at the centre of a circle.
• The perpendicular bisector of a chord passes through the centre of the circle.
• If a radius is perpendicular to a chord, then it bisects the chord and the arc it intercepts. This is known as the perpendicular bisector theorem.
• When the subtended angles by a chord are equal then the length of chords are also equal.
• If two chords in a circle intersect, then the product of the segments of one chord is equal to the product of the segments of the other chord. This is known as the intersecting chords theorem.
• The angle subtended by a chord at the centre is twice the angle subtended by the chord at the circumference.

Read More,

• Equation of a Circle
• Area of a Circle
• Circumference of Circle

Solved Probelms on Chord of a Circle

Problem 1: A circle is an angle of 70 degrees whose radius is 5cm. Calculate the chord length of the circle.

Solution:

Given

• Radius = 5 cm
• Angle =  70°

Now,

chord length = 2R × Sin [angle/2]

                    = 2 × 5 × sin [70/2]

                    = 10 × sin35°

= 10 × 0.5736

                    = 5.73cm

Problem 2: In a circle, the radius is 7cm and the perpendicular distance from the centre of the circle to its chords is 6cm. Calculate the length of the chord.

Solution:

Given

• Radius = 7 cm
• Distance = 6 cm

Now, 

Length of the chord = 2 √r² – d²

                               = 2 √7² – 6²

                               = 2 √ 49- 36

                               = 2 √13cm

Problem 3: A circle is an angle of 60 degrees whose radius is 12cm. Calculate the chord length of the circle.

Solution:

Given

• Radius = 12 cm
• Angle = 60°

Now,

chord length = 2R × Sin [angle/2]

⇒ 2 × 12 × sin [60/2]

⇒ 24 × sin30°   

⇒ 24 × 0.5

⇒ 12cm

Problem 4: In a circle, the radius is 16cm and the perpendicular distance from the centre of the circle to its chords is 5cm. Calculate the length of the chord.

Solution:

Given

• Radius = 16 cm
• Distance = 5 cm

Now,

Length of Chord = 2 √r²– d²

⇒ 2 √(16)² – (5)²

⇒ 2 √ 256- 25

⇒ 2 √231

⇒ 2 × 15.1

⇒ 30.2cm

Problem 6: Calculate the length of a common chord between the circles of radius 6cm and 5cm respectively. And, the distance between the two centres was measured to be 8cm.

Solution:

Given

Distance between the two centers = 8cm

Radius of the two circles is R₁ and R₂ with lengths 6cm and 5cm respectively

Now,

Length of a common chord of two circles = (2R₁ × R₂) / Distance between two centers of circles

⇒ 2 × 5 × 6/8

⇒ 60/8

⇒ 7.5 cm

FAQs on Chord of a Circle

Define Chord.

A line segment joining two points on the circumference of the circle is known as Chord.

What is Chord Length Formula?

The Chord Length Formula calculates the length of a chord in a circle.

Can Length of a Chord be Greater than the Diameter of a Circle?

No, the length of a chord can’t be greater than the diameter as the diameter is the longest chord of the circle.

How is the Length of a Chord Affected if it is Closer to the Centre of the Circle?

As the chord approaches the center of the circle it’s length approaches to maximum length i.e., diameter. 

How is the Length of a Chord Affected if it is Closer to the Edge of the Circle?

As the chord approaches the edge of the circle it’s length approaches to 0. Thus, the length of the chord and its distance from the edge have an inverse relation.

What is the Relationship between the Chord Length and the Central Angle of a Circle?

The relationship between the e chord length and the central angle of a circle is as follows:

Chord Length = 2r × sin [θ/2]

Where, 

• θ is the angle subtended by the chord at the center, and 
• r is the radius of the circle.

Can the Chord Length Formula be used for any Circle?

Yes, the Chord Length Formula can be used for any circle, as long as the radius and central angle are known.

Is the Diameter a Chord of a Circle?

Yes, the diameter is a chord of a circle. It is the longest chord possible of a circle. It is equal to twice the radius of the circle.

D = 2r

Where,

• D is the Diameter of the Circle
• r is the Radius of the Circle