Chiliagon Number
Last Updated :
13 Apr, 2021
Given a number N, the task is to find Nth chiliagon number.
A chiliagon number is class of figurate number. It has 1000 – sided polygon called chiliagon. The N-th chiliagon number count’s the 1000 number of dots and all others dots are surrounding with a common sharing corner and make a pattern. The first few chiliagonol numbers are 1, 1000, 2997, 5992 …
Examples:
Input: N = 2
Output: 1000
Explanation:
The second chiliagonol number is 1000.
Input: N = 3
Output: 2997

Approach: The N-th chiliagon number is given by the formula:
- Nth term of s sided polygon =
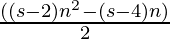
- Therefore Nth term of 1000 sided polygon is

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int chiliagonNum(int n)
{
return (998 * n * n - 996 * n) / 2;
}
int main()
{
int n = 3;
cout <<"3rd chiliagon Number is = "
<< chiliagonNum(n);
return 0;
}
|
C
#include <stdio.h>
#include <stdlib.h>
int chiliagonNum(int n)
{
return (998 * n * n - 996 * n) / 2;
}
int main()
{
int n = 3;
printf("3rd chiliagon Number is = %d",
chiliagonNum(n));
return 0;
}
|
Java
class GFG{
static int chiliagonNum(int n)
{
return (998 * n * n - 996 * n) / 2;
}
public static void main(String[] args)
{
int n = 3;
System.out.println("3rd chiliagon Number is = " +
chiliagonNum(n));
}
}
|
Python3
def chiliagonNum(n):
return (998 * n * n - 996 * n) // 2;
n = 3;
print("3rd chiliagon Number is = ",
chiliagonNum(n));
|
C#
using System;
class GFG{
static int chiliagonNum(int n)
{
return (998 * n * n - 996 * n) / 2;
}
public static void Main()
{
int n = 3;
Console.Write("3rd chiliagon Number is = " +
chiliagonNum(n));
}
}
|
Javascript
<script>
function chiliagonNum( n)
{
return (998 * n * n - 996 * n) / 2;
}
let n = 3;
document.write("3rd chiliagon Number is "
+ chiliagonNum(n));
</script>
|
Output: 3rd chiliagon Number is = 2997
Time Complexity: O(1)
Auxiliary Space: O(1)
Reference: https://en.wikipedia.org/wiki/Chiliagon
Share your thoughts in the comments
Please Login to comment...