Check for star graph

Difficulty Level : Basic
Last Updated : 03 May, 2021

You are given an n * n matrix which represents a graph with n-vertices, check whether the input matrix represents a star graph or not.
Example:

Input : Mat[][] = {{0, 1, 0},
                   {1, 0, 1},
                   {0, 1, 0}}
Output : Star graph

Input : Mat[][] = {{0, 1, 0},
                   {1, 1, 1},
                   {0, 1, 0}}
Output : Not a Star graph

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

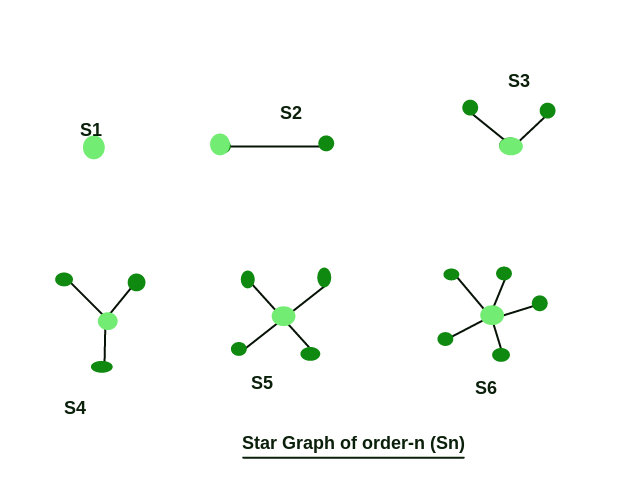
Star graph: Star graph is a special type of graph in which n-1 vertices have degree 1 and a single vertex have degree n – 1. This looks like n – 1 vertex is connected to a single central vertex. A star graph with total n – vertex is termed as Sn.
Here is an illustration for the star graph :

Approach: Just traverse whole matrix and record the number of vertices having degree 1 and degree n-1. If number of vertices having degree 1 is n-1 and number of vertex having degree n-1 is 1 then our graph should be a star graph other-wise it should be not.
Note:

For S1, there must be only one vertex with no edges.
For S2, there must be two vertices each with degree one or can say, both are connected by a single edge.
For Sn (n>2) simply check the above-explained criteria.

C++

// CPP to find whether given graph is star or not
#include<bits/stdc++.h>
using namespace std;
 
// define the size of incidence matrix
#define size 4
 
// function to find star graph
bool checkStar(int mat[][size])
{
    // initialize number of vertex
    // with deg 1 and n-1
    int vertexD1 = 0, vertexDn_1 = 0;
 
    // check for S1
    if (size == 1)
        return (mat[0][0] == 0);
     
    // check for S2
    if (size == 2)   
       return (mat[0][0] == 0 && mat[0][1] == 1 &&
               mat[1][0] == 1 && mat[1][1] == 0 );
 
    // check for Sn (n>2)
    for (int i = 0; i < size; i++)
    {
        int degreeI = 0;
        for (int j = 0; j < size; j++)
            if (mat[i][j])
                degreeI++;
 
        if (degreeI == 1)
            vertexD1++;
        else if (degreeI == size-1)
            vertexDn_1++;
    }
     
    return (vertexD1 == (size-1) &&
            vertexDn_1 == 1);
}
 
// driver code
int main()
{
    int mat[size][size] = { {0, 1, 1, 1},
                            {1, 0, 0, 0},
                            {1, 0, 0, 0},
                            {1, 0, 0, 0}};
 
    checkStar(mat) ? cout << "Star Graph" :
                     cout << "Not a Star Graph";
    return 0;
}

Java

// Java program to find whether
// given graph is star or not
import java.io.*;
 
class GFG
{
    // define the size of
    // incidence matrix
    static int size = 4;
     
    // function to find
    // star graph
    static boolean checkStar(int mat[][])
    {
        // initialize number of
        // vertex with deg 1 and n-1
        int vertexD1 = 0,
            vertexDn_1 = 0;
     
        // check for S1
        if (size == 1)
            return (mat[0][0] == 0);
         
        // check for S2
        if (size == 2)
        return (mat[0][0] == 0 &&
                mat[0][1] == 1 &&
                mat[1][0] == 1 &&
                mat[1][1] == 0);
     
        // check for Sn (n>2)
        for (int i = 0; i < size; i++)
        {
            int degreeI = 0;
            for (int j = 0; j < size; j++)
                if (mat[i][j] == 1)
                    degreeI++;
     
            if (degreeI == 1)
                vertexD1++;
            else if (degreeI == size - 1)
                vertexDn_1++;
        }
         
        return (vertexD1 == (size - 1) &&
                vertexDn_1 == 1);
    }
     
    // Driver code
    public static void main(String args[])
    {
        int mat[][] = {{0, 1, 1, 1},
                       {1, 0, 0, 0},
                       {1, 0, 0, 0},
                       {1, 0, 0, 0}};
     
        if (checkStar(mat))
            System.out.print("Star Graph");
        else
            System.out.print("Not a Star Graph");
    }
}
 
// This code is contributed by
// Manish Shaw(manishshaw1)

Python3

# Python to find whether
# given graph is star
# or not
 
# define the size
# of incidence matrix
size = 4
 
# def to
# find star graph
def checkStar(mat) :
 
    global size
     
    # initialize number of
    # vertex with deg 1 and n-1
    vertexD1 = 0
    vertexDn_1 = 0
 
    # check for S1
    if (size == 1) :
        return (mat[0][0] == 0)
     
    # check for S2
    if (size == 2) :
        return (mat[0][0] == 0 and
                mat[0][1] == 1 and
                mat[1][0] == 1 and
                mat[1][1] == 0)
 
    # check for Sn (n>2)
    for i in range(0, size) :
 
        degreeI = 0
        for j in range(0, size) :
            if (mat[i][j]) :
                degreeI = degreeI + 1
 
        if (degreeI == 1) :
            vertexD1 = vertexD1 + 1
 
        elif (degreeI == size - 1):
            vertexDn_1 = vertexDn_1 + 1
     
    return (vertexD1 == (size - 1) and
            vertexDn_1 == 1)
 
# Driver code
mat = [[0, 1, 1, 1],
       [1, 0, 0, 0],
       [1, 0, 0, 0],
       [1, 0, 0, 0]]
  
if(checkStar(mat)) :
    print ("Star Graph")
else :
    print ("Not a Star Graph")
     
# This code is contributed by
# Manish Shaw(manishshaw1)

C#

// C# to find whether given
// graph is star or not
using System;
 
class GFG
{
    // define the size of
    // incidence matrix
    static int size = 4;
     
    // function to find
    // star graph
    static bool checkStar(int [,]mat)
    {
        // initialize number of
        // vertex with deg 1 and n-1
        int vertexD1 = 0, vertexDn_1 = 0;
     
        // check for S1
        if (size == 1)
            return (mat[0, 0] == 0);
         
        // check for S2
        if (size == 2)
        return (mat[0, 0] == 0 &&
                mat[0, 1] == 1 &&
                mat[1, 0] == 1 &&
                mat[1, 1] == 0);
     
        // check for Sn (n>2)
        for (int i = 0; i < size; i++)
        {
            int degreeI = 0;
            for (int j = 0; j < size; j++)
                if (mat[i, j] == 1)
                    degreeI++;
     
            if (degreeI == 1)
                vertexD1++;
            else if (degreeI == size - 1)
                vertexDn_1++;
        }
         
        return (vertexD1 == (size - 1) &&
                vertexDn_1 == 1);
    }
     
    // Driver code
    static void Main()
    {
        int [,]mat = new int[4, 4]{{0, 1, 1, 1},
                                   {1, 0, 0, 0},
                                   {1, 0, 0, 0},
                                   {1, 0, 0, 0}};
     
        if (checkStar(mat))
            Console.Write("Star Graph");
        else
            Console.Write("Not a Star Graph");
    }
}
// This code is contributed by
// Manish Shaw(manishshaw1)

PHP

<?php
// PHP to find whether
// given graph is star
// or not
 
// define the size
// of incidence matrix
$size = 4;
 
// function to
// find star graph
function checkStar($mat)
{
    global $size;
     
    // initialize number of
    // vertex with deg 1 and n-1
    $vertexD1 = 0;
    $vertexDn_1 = 0;
 
    // check for S1
    if ($size == 1)
        return ($mat[0][0] == 0);
     
    // check for S2
    if ($size == 2)
    return ($mat[0][0] == 0 &&
            $mat[0][1] == 1 &&
            $mat[1][0] == 1 &&
            $mat[1][1] == 0 );
 
    // check for Sn (n>2)
    for ($i = 0; $i < $size; $i++)
    {
        $degreeI = 0;
        for ($j = 0; $j < $size; $j++)
            if ($mat[$i][$j])
                $degreeI++;
 
        if ($degreeI == 1)
            $vertexD1++;
        else if ($degreeI == $size - 1)
            $vertexDn_1++;
    }
     
    return ($vertexD1 == ($size - 1) &&
            $vertexDn_1 == 1);
}
 
// Driver code
$mat = array(array(0, 1, 1, 1),
             array(1, 0, 0, 0),
             array(1, 0, 0, 0),
             array(1, 0, 0, 0));
 
if(checkStar($mat))
    echo ("Star Graph");
else
    echo ("Not a Star Graph");
     
// This code is contributed by
// Manish Shaw(manishshaw1)
?>

Javascript

<script>
 
// Javascript to find whether given
// graph is star or not
 
// define the size of incidence matrix
var size = 4;
 
// function to find star graph
function checkStar( mat)
{
    // initialize number of vertex
    // with deg 1 and n-1
    var vertexD1 = 0, vertexDn_1 = 0;
 
    // check for S1
    if (size == 1)
        return (mat[0][0] == 0);
     
    // check for S2
    if (size == 2)   
       return (mat[0][0] == 0 && mat[0][1] == 1 &&
               mat[1][0] == 1 && mat[1][1] == 0 );
 
    // check for Sn (n>2)
    for (var i = 0; i < size; i++)
    {
        var degreeI = 0;
        for (var j = 0; j < size; j++)
            if (mat[i][j])
                degreeI++;
 
        if (degreeI == 1)
            vertexD1++;
        else if (degreeI == size-1)
            vertexDn_1++;
    }
     
    return (vertexD1 == (size-1) &&
            vertexDn_1 == 1);
}
 
// driver code
var mat = [ [0, 1, 1, 1],
                        [1, 0, 0, 0],
                        [1, 0, 0, 0],
                        [1, 0, 0, 0]];
checkStar(mat) ? document.write( "Star Graph") :
                 document.write( "Not a Star Graph");
 
</script>

Output:

Star Graph

My Personal Notes

Related Articles

Related Articles

Check for star graph

C++

Java

Python3

C#

PHP

Javascript