Check if it is possible to perform the given Grid Division
Last Updated :
28 Mar, 2022
Given two integers N and M which represent the size of a grid. Also given an integer array arr[] of size P which represent that the given grid is divided into P parts each consisting of arr[i] cells from the grid. The task is to check whether it is possible to divide the grid in the given manner or not.
Examples:
Input: arr[] = {6, 3, 2, 1}, N = 3, M = 4
Output: Yes
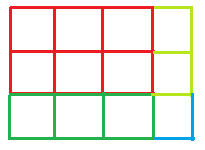
Input: arr[] = {4, 2, 2}, N = 3, M = 2
Output: No
Approach: In order for the division to be possible, the sum of the cells of all the parts must be equal to the total number of cells in the given grid i.e. the sum of all the array elements must be equal to N * M.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool isPossible(int arr[], int p, int n, int m)
{
int sum = 0;
for (int i = 0; i < p; i++)
sum += arr[i];
if (sum == (n * m))
return true;
return false;
}
int main()
{
int n = 3, m = 4;
int arr[] = { 6, 3, 2, 1 };
int p = sizeof(arr) / sizeof(arr[0]);
if (isPossible(arr, p, n, m))
cout << "Yes";
else
cout << "No";
return 0;
}
|
Java
import java.util.*;
class GFG
{
static boolean isPossible(int arr[], int p,
int n, int m)
{
int sum = 0;
for (int i = 0; i < p; i++)
sum += arr[i];
if (sum == (n * m))
return true;
return false;
}
public static void main(String[] args)
{
int n = 3, m = 4;
int arr[] = { 6, 3, 2, 1 };
int p = arr.length;
if (isPossible(arr, p, n, m))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def isPossible(arr, p, n, m):
sum = 0;
for i in range(p):
sum += arr[i];
if (sum == (n * m)):
return True;
return False;
if __name__ == '__main__':
n = 3;
m = 4;
arr = [6, 3, 2, 1];
p = len(arr);
if (isPossible(arr, p, n, m)):
print("Yes");
else:
print("No");
|
C#
using System;
class GFG
{
static bool isPossible(int []arr, int p,
int n, int m)
{
int sum = 0;
for (int i = 0; i < p; i++)
sum += arr[i];
if (sum == (n * m))
return true;
return false;
}
public static void Main(String[] args)
{
int n = 3, m = 4;
int []arr = { 6, 3, 2, 1 };
int p = arr.Length;
if (isPossible(arr, p, n, m))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
function isPossible(arr, p, n, m)
{
var sum = 0;
for (var i = 0; i < p; i++)
sum += arr[i];
if (sum == (n * m))
return true;
return false;
}
var n = 3, m = 4;
var arr = [ 6, 3, 2, 1 ];
var p = arr.length;
if (isPossible(arr, p, n, m))
document.write( "Yes");
else
document.write( "No");
</script>
|
Time Complexity: O(p)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...