Cayley’s Formula
Last Updated :
28 Jan, 2021
Cayley’s Formula: This formula tells how many trees can be constructed with N vertices. It states that there are NN – 2 labeled trees that of N nodes. The nodes are labeled from 1, 2, …, N, and two trees are different if either their structure or labeling is different.
For Example: When N is 4, the number of labeled trees is 44 – 2 = 16.
Below is the image depicting the number of labeled trees:

In the above image, there are 4 nodes given from which 16 labeled trees are created.
Cayley’s formula derived using Prüfer Codes:
Prüfer Code:
- A Prüfer Code is a sequence of (N – 2) numbers that describes a labeled tree.
- The code is constructed by following a process that removes (N – 2) leaves from the tree.
- At each step, the leaf with the smallest label is removed, and the label of its only neighbor is added to the code.
Below are the steps to calculate the Prüfer Code of the following graph:
- Given a graph with five nodes:
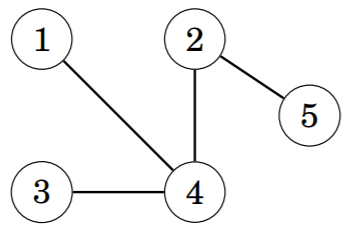
- Remove node 1 and add node 4 to the code:

- Then remove node 3 and add node 4 to the code:

- Finally, remove node 4 and add node 2 to the code:
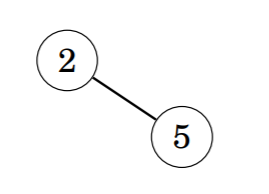
Thus, the Prüfer code of the graph is given by {4, 4, 2}.
- Prüfer code can be constructed for any tree.
- The original tree can be reconstructed from a Prüfer code.
- Hence, the number of labeled trees of n nodes equals NN – 2 , the number of Prüfer codes of size N.
Share your thoughts in the comments
Please Login to comment...