Calculate Sum of ratio of special characters to length of substrings of the given string
Last Updated :
06 Oct, 2022
Given a string str and an array of special characters, specialArray[], the task is to find the sum of the ratio of the count of special characters to the length of the substring for all possible substring of the given string.
Ratio of count of special characters in a substring to the length of substrings of the given string is given by
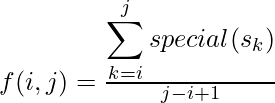
Sum of the ratios calculated above is given by
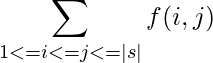
Examples:
Input: str = “abcdabc”, specialArray[] = {‘a’, ‘b’, ‘c’, ‘d’}
Output: 28.00000
Explanation:
Length of string = 7
Count of all possible substrings = (7 * (8 + 1)) / 2 = 28
Since, all the characters of the string are included in specialArray[], ratio of count of special characters to the length of substring for every substring will always be 1.
Hence, the sum of ratio = Number of substrings * 1 = 28.
Input: str = “abcd”, specialArray[] = {‘b’, ‘c’}
Output: 5.83333
Approach:
Follow the steps below to solve the problem:
- For every possible length of substrings from 1 to N, find the count of special characters in every substring of length x and add the ratio of count and x to the answer.
- To find the count of special characters in each substring in constant time, create a prefix sum array of the count of special characters using the relation:
prefix[i] = prefix[i – 1] + special(s[i]);
- Calculate the count of special characters in a substring within the indices [i, j] is given by the relation:
prefix[j – 1] – prefix[i – 1]
Therefore, the ratio of the count of special characters to the length of substring,
f(i, j) = (prefix[j – 1] – prefix[i – 1])/(j – i + 1)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
vector<int> prefix(N, 0);
vector<int> sum(N, 0);
bool isSpecial(char c,
vector<char>& special)
{
for (auto& i : special)
if (i == c)
return true;
return false;
}
double countRatio(string& s,
vector<char>& special)
{
int n = s.length();
for (int i = 0; i < n; i++) {
prefix[i] = int(isSpecial(s[i],
special));
if (i > 0)
prefix[i] += prefix[i - 1];
}
for (int i = 0; i < n; i++) {
sum[i] = prefix[i];
if (i > 0)
sum[i] += sum[i - 1];
}
double ans = 0;
for (int i = 1; i <= n; i++) {
int count = sum[n - 1]
- (i > 1 ? sum[i - 2] : 0);
count
-= (i < n ? sum[n - i - 1] : 0);
ans += double(count) / double(i);
}
return ans;
}
int main()
{
string s = "abcd";
vector<char> special = { 'b', 'c' };
double ans = countRatio(s, special);
cout << fixed << setprecision(6)
<< ans << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static int N = 1000000 + 5;
static int []prefix = new int[N];
static int []sum = new int[N];
static int isSpecial(char c,
char[] special)
{
for (char i : special)
if (i == c)
return 1;
return 0;
}
static double countRatio(char []s,
char[] special)
{
int n = s.length;
for (int i = 0; i < n; i++)
{
prefix[i] = (isSpecial(s[i],
special));
if (i > 0)
prefix[i] += prefix[i - 1];
}
for (int i = 0; i < n; i++)
{
sum[i] = prefix[i];
if (i > 0)
sum[i] += sum[i - 1];
}
double ans = 0;
for (int i = 1; i <= n; i++)
{
int count = sum[n - 1] - (i > 1 ?
sum[i - 2] : 0);
count -= (i < n ?
sum[n - i - 1] : 0);
ans += (double)count / (double)i;
}
return ans;
}
public static void main(String[] args)
{
String s = "abcd";
char[] special = {'b', 'c'};
double ans = countRatio(s.toCharArray(),
special);
System.out.format("%.6f",ans);
}
}
|
Python3
N = 100005
prefix = [0] * N
sum = [0] * N
def isSpecial(c, special):
for i in special:
if (i == c):
return True
return False
def countRatio(s, special):
n = len(s)
for i in range(n):
prefix[i] = int(isSpecial(s[i],
special))
if (i > 0):
prefix[i] += prefix[i - 1]
for i in range(n):
sum[i] = prefix[i]
if (i > 0):
sum[i] += sum[i - 1]
ans = 0
for i in range(1, n + 1):
if i > 1:
count = sum[n - 1]- sum[i - 2]
else:
count = sum[n - 1]
if i < n:
count -= sum[n - i - 1]
ans += count / i
return ans
if __name__ == "__main__":
s = "abcd"
special = [ 'b', 'c' ]
ans = countRatio(s, special)
print('%.6f' % ans)
|
C#
using System;
class GFG{
static int N = 1000000 + 5;
static int []prefix = new int[N];
static int []sum = new int[N];
static int isSpecial(char c,
char[] special)
{
foreach(char i in special)
if (i == c)
return 1;
return 0;
}
static double countRatio(char []s,
char[] special)
{
int n = s.Length;
for(int i = 0; i < n; i++)
{
prefix[i] = (isSpecial(s[i],
special));
if (i > 0)
prefix[i] += prefix[i - 1];
}
for(int i = 0; i < n; i++)
{
sum[i] = prefix[i];
if (i > 0)
sum[i] += sum[i - 1];
}
double ans = 0;
for(int i = 1; i <= n; i++)
{
int count = sum[n - 1] - (i > 1 ?
sum[i - 2] : 0);
count -= (i < n ?
sum[n - i - 1] : 0);
ans += (double)count / (double)i;
}
return ans;
}
public static void Main(String[] args)
{
String s = "abcd";
char[] special = {'b', 'c'};
double ans = countRatio(s.ToCharArray(),
special);
Console.WriteLine("{0:F6}", ans);
}
}
|
Javascript
<script>
var N = 1000005;
var prefix = Array(N).fill(0);
var sum = Array(N).fill(0);
function isSpecial(c, special)
{
var ans = false;
special.forEach(i => {
if (i == c)
ans =true;
});
return ans;
}
function countRatio(s, special)
{
var n = s.length;
for(var i = 0; i < n; i++)
{
prefix[i] = (isSpecial(s[i],
special));
if (i > 0)
prefix[i] += prefix[i - 1];
}
for(var i = 0; i < n; i++)
{
sum[i] = prefix[i];
if (i > 0)
sum[i] += sum[i - 1];
}
var ans = 0;
for(var i = 1; i <= n; i++)
{
var count = sum[n - 1] -
((i > 1) ? sum[i - 2] : 0);
count -= ((i < n) ? sum[n - i - 1] : 0);
ans += ((count) / (i));
}
return ans;
}
var s = "abcd";
var special = [ 'b', 'c' ];
var ans = countRatio(s.split(''), special);
document.write( ans.toFixed(6));
</script>
|
Time Complexity: O(N)
Space Complexity: O(N)
Share your thoughts in the comments
Please Login to comment...