C# | Exception

An exception is an unwanted or unexpected event, which occurs during the execution of a program i.e at runtime, that disrupts the normal flow of the program’s instructions. Sometimes during the execution of the program, the user may face the possibility that the program may crash or show an unexpected event during its runtime execution. This unwanted event is known as Exception and it generally gives the indication regarding something wrong within the code.

Example: To show the occurrence of exception during divide by zero operation as follows:

// C# program to illustrate the exception
using System;
class Geeks {

        // Main Method
        static void Main(string[] args)
        {

            // taking two integer value
            int A = 12;
            int B = 0;

            // divide by zero error
            int c = A / B;

            Console.Write("Value of C is " + c);

        }
}

Runtime Error:

Unhandled Exception:
System.DivideByZeroException: Attempted to divide by zero.
at Geeks.Main (System.String[] args) <0x4068cd50 + 0x0000c> in :0
[ERROR] FATAL UNHANDLED EXCEPTION: System.DivideByZeroException: Attempted to divide by zero.
at Geeks.Main (System.String[] args) <0x4068cd50 + 0x0000c> in :0

Difference between Errors and Exception

Errors:

• Errors are unexpected issues that may arise during computer program execution.
• Errors cannot be handled.
• All Errors are exceptions.

Exceptions:

• Exceptions are unexpected events that may arise during run-time.
• Exceptions can be handled using try-catch mechanisms.
• All exceptions are not errors.

Exception Hierarchy

In C#, all the exceptions are derived from the base class Exception which gets further divided into two branches as ApplicationException and another one is SystemException. SystemException is a base class for all CLR or program code generated errors. ApplicationException is a base class for all application related exceptions. All the exception classes are directly or indirectly derived from the Exception class. In case of ApplicationException, the user may create its own exception types and classes. But SystemException contains all the known exception types such as DivideByZeroException or NullReferenceException etc.

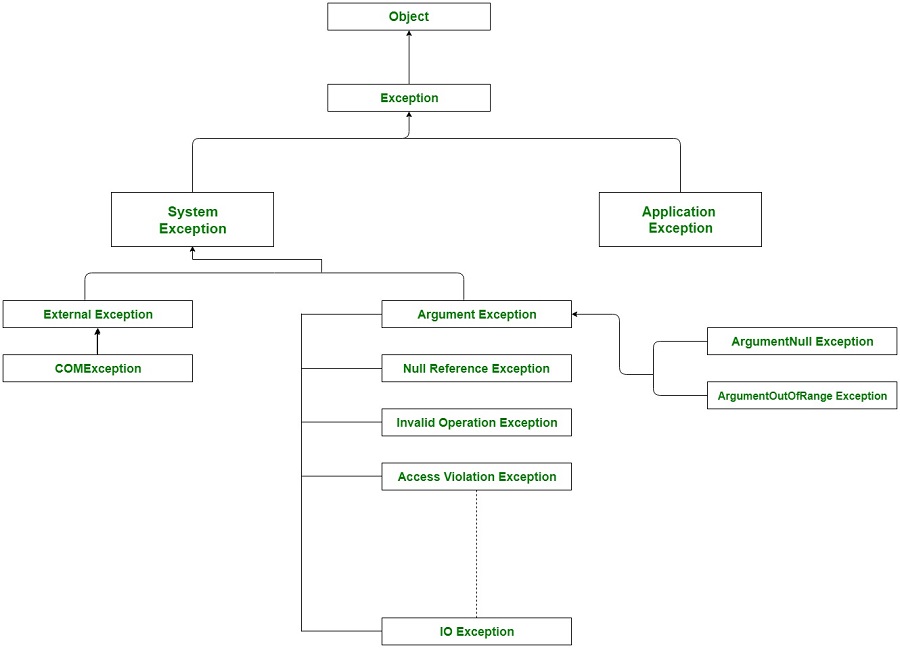
Different Exception Classes: There are different kinds of exceptions which can be generated in C# program:

• Divide By Zero exception: It occurs when the user attempts to divide by zero
• Out of Memory exceptions: It occurs when then the program tries to use excessive memory
• Index out of bound Exception: Accessing the array element or index which is not present in it.
• Stackoverflow Exception: Mainly caused due to infinite recursion process
• Null Reference Exception : Occurs when the user attempts to reference an object which is of NULL type.

…..and many more.

Properties of the Exception Class: The Exception class has many properties which help the user to get information about the exception during the exception.

• Data: This property helps to get the information about the arbitrary data which is held by the property in the key-value pairs.
• TargetSite: This property helps to get the name of the method where the exception will throw.
• Message: This property helps to provide the details about the main cause of the exception occurrence.
• HelpLink: This property helps to hold the URL for a particular exception.
• StackTrace: This property helps to provide the information about where the error occurred.
• InnerException: This property helps to provide the information about the series of exceptions that might have occurred.