Bubble Sort in C++

Bubble Sort Algorithm is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity is quite high.

Bubble Sort in C++

Bubble Sort Example

Consider an array to be mentioned below:

arr[] = {5, 1, 4, 2, 8}

First Traversing 

Bubble sort starts with very first two elements, comparing them to check which one is greater.

• ( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1. 
• ( 1 5 4 2 8 ) –>  ( 1 4 5 2 8 ), Swap since 5 > 4 
• ( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 ), Swap since 5 > 2 
• ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.

Second Traversing

Now, during second iteration it should look like this:

• ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ) 
• ( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2 
• ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
• ( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 ) 

Third Traversing

Now, the array is already sorted, but our algorithm does not know if it is completed.

The algorithm needs one whole pass without any swap to know it is sorted.

• ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
• ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
• ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
• ( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 

Output:

// Sorted
arr=[1,2,4,5,8]

Bubble Sort Program

Following are the implementations of Bubble Sort

C++

// C++ program for implementation
// of Bubble sort
#include <bits/stdc++.h>
using namespace std;

// A function to implement bubble sort
void bubbleSort(int arr[], int n)
{
    int i, j;
    for (i = 0; i < n - 1; i++)

        // Last i elements are already
        // in place
        for (j = 0; j < n - i - 1; j++)
            if (arr[j] > arr[j + 1])
                swap(arr[j], arr[j + 1]);
}

// Function to print an array
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        cout << arr[i] << " ";
    cout << endl;
}

// Driver code
int main()
{
    int arr[] = { 5, 1, 4, 2, 8};
    int N = sizeof(arr) / sizeof(arr[0]);
    bubbleSort(arr, N);
    cout << "Sorted array: \n";
    printArray(arr, N);
    return 0;
}

Output

Sorted array: 
1 2 4 5 8 

Optimized Implementation of Bubble Sort:

• The above function always runs O(n^2) time even if the array is sorted.
• It can be optimized by stopping the algorithm if the inner loop didn’t cause any swap. 

Below is the implementation for the above approach: 

C++

// Optimized implementation of Bubble sort
#include <bits/stdc++.h>
using namespace std;

// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n) {
    bool isUnsorted;
    do {
        isUnsorted = false;
        for (int i = 0; i < (n - 1); i++) {
            if (arr[i] > arr[i + 1]) {
                isUnsorted = true;
                for (; i < (n - 1); i++) {
                    if (arr[i] > arr[i + 1]) {
                        std::swap(arr[i], arr[i + 1]);
                    }
                }
            }
        }
    } while (isUnsorted);
}

// Function to print an array
void printArray(int arr[], int size)
{
    int i;
    for (i = 0; i < size; i++)
        cout <<" "<< arr[i];
}

// Driver program to test above functions
int main()
{
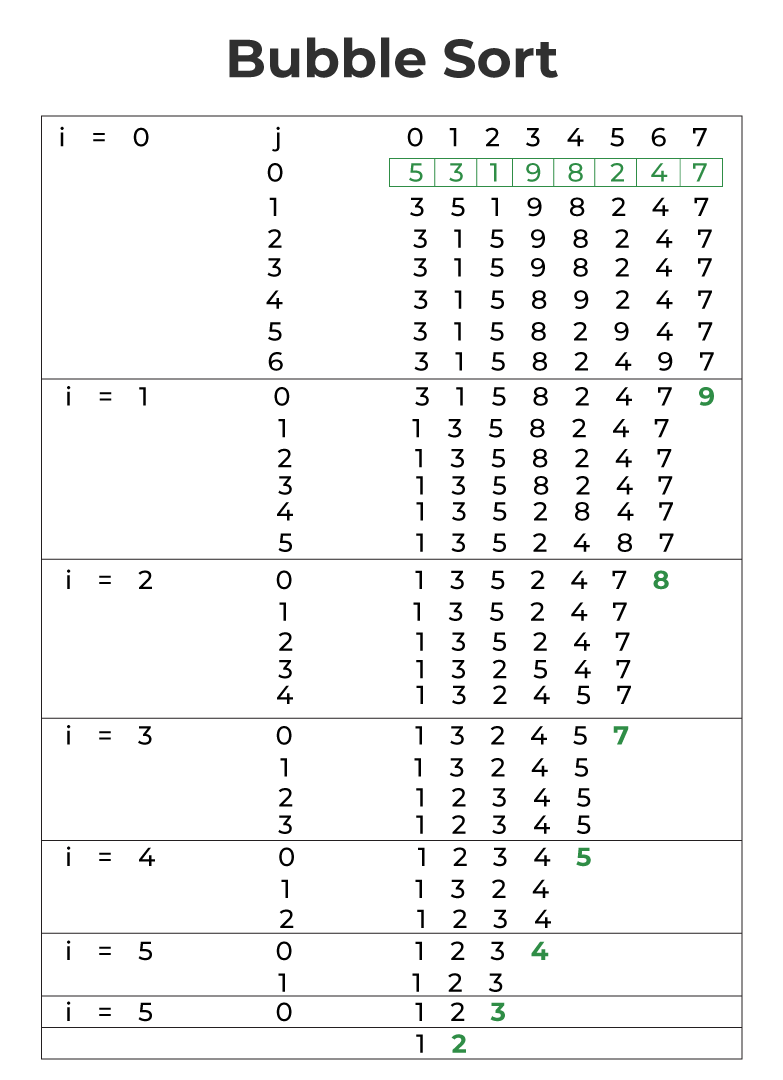
    int arr[] = {5, 3, 1, 9, 8, 2, 4, 7};
    int N = sizeof(arr)/sizeof(arr[0]);
    bubbleSort(arr, N);
    cout <<"Sorted array: \n";
    printArray(arr, N);
    return 0;
}
// This code is contributed by shivanisinghss2110

Output

Sorted array: 
 1 2 3 4 5 7 8 9

Time Complexity: O(N²)
Auxiliary Space: O(1)

Worst Case Analysis for Bubble Sort

The worst-case condition for bubble sort occurs when elements of the array are arranged in decreasing order.
In the worst case, the total number of iterations or passes required to sort a given array is (n-1). where ‘n’ is the number of elements present in the array.

At pass 1 :  Number of comparisons = (n-1)
                     Number of swaps = (n-1)

At pass 2 :  Number of comparisons = (n-2)
                     Number of swaps = (n-2)

At pass 3 :  Number of comparisons = (n-3)
                    Number of swaps = (n-3)
.
                              .
                              .
At pass n-1 :  Number of comparisons = 1
                        Number of swaps = 1

Now , calculating total number of comparison required to sort the array
= (n-1) + (n-2) +  (n-3) + . . . 2 + 1
= (n-1)*(n-1+1)/2  { by using sum of N natural Number formula }
= n (n-1)/2 

For the Worst case:

Total number of swaps = Total number of comparison
Total number of comparison (Worst case) = n(n-1)/2
Total number of swaps (Worst case) = n(n-1)/2

Worst and Average Case Time Complexity: O(N²). The worst case occurs when an array is reverse sorted.

Best Case Time Complexity: O(N). The best case occurs when an array is already sorted.

Auxiliary Space: O(1)

Frequently Asked Questions

1. What is the Boundary Case for Bubble sort?

Bubble sort takes minimum time (Order of n) when elements are already sorted. Hence it is best to check if the array is already sorted or not beforehand, to avoid O(N²) time complexity.

2. Does sorting happens in place in Bubble sort?

Yes, Bubble sort performs the swapping of adjacent pairs without the use of any major data structure. Hence Bubble sort algorithm is an in-place algorithm.

3. Is Bubble sort algorithm stable?

Yes, the bubble sort algorithm is stable.

4. Where is Bubble sort algorithm used?

Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm. 
In computer graphics, it is popular for its capability to detect a very small error (like a swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n). 

Please refer complete article on Bubble Sort for more details!