Python | Box-Cox Transformation
Last Updated :
13 May, 2022
Imagine you are watching a horse race and like any other race, there are fast runners and slow runners. So, logically speaking, the horse which came first and the fast horses along with it will have the smaller difference of completion time whereas the slowest ones will have a larger difference in their completion time.
We can relate this to a very famous term in statistics called variance which refers to how much is the data varying with respect to the mean. Here in our example, there is an inconsistent variance (Heteroscedasticity) between the fast horses and the slow horses because there will be small variations for shorter completion time and vice versa.
Hence, the distribution for our data will not be a bell curve or normally distributed as there will be a longer tail on the right side. These types of distributions follow Power law or 80-20 rule where the relative change in one quantity varies as the power of another. In the above plot, we can see power-law distribution which is having peaked for short running times because of the small variance and heavy tail due to longer running times. These power-law distributions are found in the field of physics, biology, economics, etc.
In the above plot, we can see power-law distribution which is having peaked for short running times because of the small variance and heavy tail due to longer running times. These power-law distributions are found in the field of physics, biology, economics, etc.
So, just think for a second that if these distributions are found in so many fields, what if we could transform it to a much comfortable distribution like normal distribution? That would make our life a lot easier. Fortunately, we have a way to transform power-law or any non-linear distribution to normal using a Box-Cox Transformation
Let us think intuitively that if we were to do this transform ourselves, how would we proceed?
It is clear from the above-shown figure that if somehow we could inflate the variability for the left-hand side of non-normal distribution i.e peak and reduce the variability at the tails. In short, trying to move the peak towards the centre then we can get a curve close to the bell-shaped curve.
Formally, A Box cox transformation is defined as a way to transform non-normal dependent variables in our data to a normal shape through which we can run a lot more tests than we could have.
Mathematics behind Box-Cox Transformation: How can we convert our intuitive thinking into a mathematical transformation function? Logarithmic transformation is all we need. When a log transformation is applied to non-normal distribution, it tries to expand the differences between the smaller values because the slope for the logarithmic function is steeper for smaller values whereas the differences between the larger values can be reduced because, for large values, log distribution has a moderate slope. That is what we thought of doing, right? Box-cox Transformation only cares about computing the value of 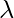 which varies from – 5 to 5. A value of
which varies from – 5 to 5. A value of 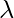 is said to be best if it is able to approximate the non-normal curve to a normal curve. The transformation equation is as follows:
is said to be best if it is able to approximate the non-normal curve to a normal curve. The transformation equation is as follows: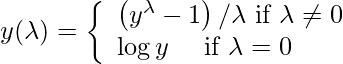 This function requires input to be positive. Using this formula manually is a very laborious task thus many popular libraries provide this function.
This function requires input to be positive. Using this formula manually is a very laborious task thus many popular libraries provide this function.
Implementation: SciPy’s stats package provides a function called boxcox for performing box-cox power transformation that takes in original non-normal data as input and returns fitted data along with the lambda value that was used to fit the non-normal distribution to normal distribution. Following is the code for the same.
Example:
Python3
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
original_data = np.random.exponential(size = 1000)
fitted_data, fitted_lambda = stats.boxcox(original_data)
fig, ax = plt.subplots(1, 2)
sns.distplot(original_data, hist = False, kde = True,
kde_kws = {'shade': True, 'linewidth': 2},
label = "Non-Normal", color ="green", ax = ax[0])
sns.distplot(fitted_data, hist = False, kde = True,
kde_kws = {'shade': True, 'linewidth': 2},
label = "Normal", color ="green", ax = ax[1])
plt.legend(loc = "upper right")
fig.set_figheight(5)
fig.set_figwidth(10)
print(f"Lambda value used for Transformation: {fitted_lambda}")
|
Output: We can see that the non-normal distribution was converted into a normal distribution or rather close to normal using the SciPy.stats.boxcox(). Does Box-cox always work? The answer is NO. Box-cox does not guarantee normality because it never checks for the normality which is necessary to be foolproof that it has correctly transformed the non-normal distribution or not. It only checks for the smallest Standard deviation.
We can see that the non-normal distribution was converted into a normal distribution or rather close to normal using the SciPy.stats.boxcox(). Does Box-cox always work? The answer is NO. Box-cox does not guarantee normality because it never checks for the normality which is necessary to be foolproof that it has correctly transformed the non-normal distribution or not. It only checks for the smallest Standard deviation.
Therefore, it is absolutely necessary to always check the transformed data for normality using a probability plot.
Share your thoughts in the comments
Please Login to comment...