Suppose you are creating an account on Geekbook, you want to enter a cool username, you entered it and got a message, “Username is already taken”. You added your birth date along username, still no luck. Now you have added your university roll number also, still got “Username is already taken”. It’s really frustrating, isn’t it?
But have you ever thought about how quickly Geekbook checks availability of username by searching millions of username registered with it. There are many ways to do this job –
- Linear search : Bad idea!
- Binary Search : Store all username alphabetically and compare entered username with middle one in list, If it matched, then username is taken otherwise figure out, whether entered username will come before or after middle one and if it will come after, neglect all the usernames before middle one(inclusive). Now search after middle one and repeat this process until you got a match or search end with no match. This technique is better and promising but still it requires multiple steps.
But, there must be something better!!
Bloom Filter is a data structure that can do this job.
For understanding bloom filters, you must know what is hashing. A hash function takes input and outputs a unique identifier of fixed length which is used for identification of input.
What is Bloom Filter?
A Bloom filter is a space-efficient probabilistic data structure that is used to test whether an element is a member of a set. For example, checking availability of username is set membership problem, where the set is the list of all registered username. The price we pay for efficiency is that it is probabilistic in nature that means, there might be some False Positive results. False positive means, it might tell that given username is already taken but actually it’s not.
Interesting Properties of Bloom Filters
- Unlike a standard hash table, a Bloom filter of a fixed size can represent a set with an arbitrarily large number of elements.
- Adding an element never fails. However, the false positive rate increases steadily as elements are added until all bits in the filter are set to 1, at which point all queries yield a positive result.
- Bloom filters never generate false negative result, i.e., telling you that a username doesn’t exist when it actually exists.
- Deleting elements from filter is not possible because, if we delete a single element by clearing bits at indices generated by k hash functions, it might cause deletion of few other elements. Example – if we delete “geeks” (in given example below) by clearing bit at 1, 4 and 7, we might end up deleting “nerd” also Because bit at index 4 becomes 0 and bloom filter claims that “nerd” is not present.
Working of Bloom Filter
A empty bloom filter is a bit array of m bits, all set to zero, like this –

We need k number of hash functions to calculate the hashes for a given input. When we want to add an item in the filter, the bits at k indices h1(x), h2(x), … hk(x) are set, where indices are calculated using hash functions.
Example – Suppose we want to enter “geeks” in the filter, we are using 3 hash functions and a bit array of length 10, all set to 0 initially. First we’ll calculate the hashes as follows:
h1(“geeks”) % 10 = 1
h2(“geeks”) % 10 = 4
h3(“geeks”) % 10 = 7
Note: These outputs are random for explanation only.
Now we will set the bits at indices 1, 4 and 7 to 1

Again we want to enter “nerd”, similarly, we’ll calculate hashes
h1(“nerd”) % 10 = 3
h2(“nerd”) % 10 = 5
h3(“nerd”) % 10 = 4
Set the bits at indices 3, 5 and 4 to 1

Now if we want to check “geeks” is present in filter or not. We’ll do the same process but this time in reverse order. We calculate respective hashes using h1, h2 and h3 and check if all these indices are set to 1 in the bit array. If all the bits are set then we can say that “geeks” is probably present. If any of the bit at these indices are 0 then “geeks” is definitely not present.
False Positive in Bloom Filters
The question is why we said “probably present”, why this uncertainty. Let’s understand this with an example. Suppose we want to check whether “cat” is present or not. We’ll calculate hashes using h1, h2 and h3
h1(“cat”) % 10 = 1
h2(“cat”) % 10 = 3
h3(“cat”) % 10 = 7
If we check the bit array, bits at these indices are set to 1 but we know that “cat” was never added to the filter. Bit at index 1 and 7 was set when we added “geeks” and bit 3 was set we added “nerd”.

So, because bits at calculated indices are already set by some other item, bloom filter erroneously claims that “cat” is present and generating a false positive result. Depending on the application, it could be huge downside or relatively okay.
We can control the probability of getting a false positive by controlling the size of the Bloom filter. More space means fewer false positives. If we want to decrease probability of false positive result, we have to use more number of hash functions and larger bit array. This would add latency in addition to the item and checking membership.
Operations that a Bloom Filter supports
- insert(x) : To insert an element in the Bloom Filter.
- lookup(x) : to check whether an element is already present in Bloom Filter with a positive false probability.
NOTE : We cannot delete an element in Bloom Filter.
Probability of False positivity: Let m be the size of bit array, k be the number of hash functions and n be the number of expected elements to be inserted in the filter, then the probability of false positive p can be calculated as:
![Rendered by QuickLaTeX.com P=\left ( 1-\left [ 1- \frac {1}{m} \right ]^{kn} \right )^k](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-80f3fa1eb1567a5887d08c7cbddf639d_l3.png)
Size of Bit Array: If expected number of elements n is known and desired false positive probability is p then the size of bit array m can be calculated as :
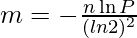
Optimum number of hash functions: The number of hash functions k must be a positive integer. If m is size of bit array and n is number of elements to be inserted, then k can be calculated as :
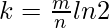
Space Efficiency
If we want to store large list of items in a set for purpose of set membership, we can store it in hashmap, tries or simple array or linked list. All these methods require storing item itself, which is not very memory efficient. For example, if we want to store “geeks” in hashmap we have to store actual string “ geeks” as a key value pair {some_key : ”geeks”}.
Bloom filters do not store the data item at all. As we have seen they use bit array which allow hash collision. Without hash collision, it would not be compact.
Choice of Hash Function
The hash function used in bloom filters should be independent and uniformly distributed. They should be fast as possible. Fast simple non cryptographic hashes which are independent enough include murmur, FNV series of hash functions and Jenkins hashes.
Generating hash is major operation in bloom filters. Cryptographic hash functions provide stability and guarantee but are expensive in calculation. With increase in number of hash functions k, bloom filter become slow. All though non-cryptographic hash functions do not provide guarantee but provide major performance improvement.
Basic implementation of Bloom Filter class in Python3. Save it as bloomfilter.py
Python
import math
import mmh3
from bitarray import bitarray
class BloomFilter(object):
def __init__(self, items_count, fp_prob):
self.fp_prob = fp_prob
self.size = self.get_size(items_count, fp_prob)
self.hash_count = self.get_hash_count(self.size, items_count)
self.bit_array = bitarray(self.size)
self.bit_array.setall(0)
def add(self, item):
digests = []
for i in range(self.hash_count):
digest = mmh3.hash(item, i) % self.size
digests.append(digest)
self.bit_array[digest] = True
def check(self, item):
for i in range(self.hash_count):
digest = mmh3.hash(item, i) % self.size
if self.bit_array[digest] == False:
return False
return True
@classmethod
def get_size(self, n, p):
m = -(n * math.log(p))/(math.log(2)**2)
return int(m)
@classmethod
def get_hash_count(self, m, n):
k = (m/n) * math.log(2)
return int(k)
|
Lets test the bloom filter. Save this file as bloom_test.py
Python
from bloomfilter import BloomFilter
from random import shuffle
n = 20
p = 0.05
bloomf = BloomFilter(n,p)
print("Size of bit array:{}".format(bloomf.size))
print("False positive Probability:{}".format(bloomf.fp_prob))
print("Number of hash functions:{}".format(bloomf.hash_count))
word_present = ['abound','abounds','abundance','abundant','accessible',
'bloom','blossom','bolster','bonny','bonus','bonuses',
'coherent','cohesive','colorful','comely','comfort',
'gems','generosity','generous','generously','genial']
word_absent = ['bluff','cheater','hate','war','humanity',
'racism','hurt','nuke','gloomy','facebook',
'geeksforgeeks','twitter']
for item in word_present:
bloomf.add(item)
shuffle(word_present)
shuffle(word_absent)
test_words = word_present[:10] + word_absent
shuffle(test_words)
for word in test_words:
if bloomf.check(word):
if word in word_absent:
print("'{}' is a false positive!".format(word))
else:
print("'{}' is probably present!".format(word))
else:
print("'{}' is definitely not present!".format(word))
|
Output
Size of bit array:124
False positive Probability:0.05
Number of hash functions:4
'war' is definitely not present!
'gloomy' is definitely not present!
'humanity' is definitely not present!
'abundant' is probably present!
'bloom' is probably present!
'coherent' is probably present!
'cohesive' is probably present!
'bluff' is definitely not present!
'bolster' is probably present!
'hate' is definitely not present!
'racism' is definitely not present!
'bonus' is probably present!
'abounds' is probably present!
'genial' is probably present!
'geeksforgeeks' is definitely not present!
'nuke' is definitely not present!
'hurt' is definitely not present!
'twitter' is a false positive!
'cheater' is definitely not present!
'generosity' is probably present!
'facebook' is definitely not present!
'abundance' is probably present!
C++ Implementation
Here is the implementation of a sample Bloom Filters with 4 sample hash functions ( k = 4) and the size of bit array is 100.
C++
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int h1(string s, int arrSize)
{
ll int hash = 0;
for (int i = 0; i < s.size(); i++)
{
hash = (hash + ((int)s[i]));
hash = hash % arrSize;
}
return hash;
}
int h2(string s, int arrSize)
{
ll int hash = 1;
for (int i = 0; i < s.size(); i++)
{
hash = hash + pow(19, i) * s[i];
hash = hash % arrSize;
}
return hash % arrSize;
}
int h3(string s, int arrSize)
{
ll int hash = 7;
for (int i = 0; i < s.size(); i++)
{
hash = (hash * 31 + s[i]) % arrSize;
}
return hash % arrSize;
}
int h4(string s, int arrSize)
{
ll int hash = 3;
int p = 7;
for (int i = 0; i < s.size(); i++) {
hash += hash * 7 + s[0] * pow(p, i);
hash = hash % arrSize;
}
return hash;
}
bool lookup(bool* bitarray, int arrSize, string s)
{
int a = h1(s, arrSize);
int b = h2(s, arrSize);
int c = h3(s, arrSize);
int d = h4(s, arrSize);
if (bitarray[a] && bitarray[b] && bitarray
&& bitarray[d])
return true;
else
return false;
}
void insert(bool* bitarray, int arrSize, string s)
{
if (lookup(bitarray, arrSize, s))
cout << s << " is Probably already present" << endl;
else
{
int a = h1(s, arrSize);
int b = h2(s, arrSize);
int c = h3(s, arrSize);
int d = h4(s, arrSize);
bitarray[a] = true;
bitarray[b] = true;
bitarray = true;
bitarray[d] = true;
cout << s << " inserted" << endl;
}
}
int main()
{
bool bitarray[100] = { false };
int arrSize = 100;
string sarray[33]
= { "abound", "abounds", "abundance",
"abundant", "accessible", "bloom",
"blossom", "bolster", "bonny",
"bonus", "bonuses", "coherent",
"cohesive", "colorful", "comely",
"comfort", "gems", "generosity",
"generous", "generously", "genial",
"bluff", "cheater", "hate",
"war", "humanity", "racism",
"hurt", "nuke", "gloomy",
"facebook", "geeksforgeeks", "twitter" };
for (int i = 0; i < 33; i++) {
insert(bitarray, arrSize, sarray[i]);
}
return 0;
}
|
Outputabound inserted
abounds inserted
abundance inserted
abundant inserted
accessible inserted
bloom inserted
blossom inserted
bolster inserted
bonny inserted
bonus inserted
bonuses inserted
coherent inserted
cohesive inserted
colorful inserted
comely inserted
comfort inserted
gems inserted
generosity inserted
generous inserted
generously inserted
genial inserted
bluff is Probably already present
cheater inserted
hate inserted
war is Probably already present
humanity inserted
racism inserted
hurt inserted
nuke is Probably already present
gloomy is Probably already present
facebook inserted
geeksforgeeks inserted
twitter inserted
Applications of Bloom filters
- Medium uses bloom filters for recommending post to users by filtering post which have been seen by user.
- Quora implemented a shared bloom filter in the feed backend to filter out stories that people have seen before.
- The Google Chrome web browser used to use a Bloom filter to identify malicious URLs
- Google BigTable, Apache HBase and Apache Cassandra, and Postgresql use Bloom filters to reduce the disk lookups for non-existent rows or columns
References
Share your thoughts in the comments
Please Login to comment...