BlackDragon – Advanced Automation Tool For Web-Recon
Last Updated :
23 Sep, 2021
Information Gathering is the process of collecting the relevant information about the target domain for increasing the scope of testing. This information consists of Subdomain Enumeration, Live Host identification, etc. This phase can be completed in an automated way. Black-Dragon is the tool used in the Web-App Information Gathering, which makes it easier to gather information about our target. Black-Dragon tool is developed in Shell Script and available on the GitHub platform, it’s open-source and free to use. Black-Dragon tool will help us in our Bug Hunting Or Web Penetration Testing Operation because it not only gathers information about the target but also arranges all this information in a structured way which makes you analyze the data in a good way.
What does This Tool Do?
- Performs Subdomain Enumeration by using Subfinder, Sublist3r, Amass, Assetfinder, KnockPy tool.
- Getting The Whole Subdomain Gathered Then Filter The Unique Domains And Extract The Only Live Subdomain Using httprobe tool.
- Fuzzing The Application Target Based Using: Gobuster, Dirsearch, Dirb tools.
- Endpoints Gathering Using Waybackurls, github-endpoints. tools.
- DNS Information Gathering Using DNSMap, DNSEnum, MassDNS tools
Installation of BlackDragon Tool on Kali Linux OS
Step 1: Use the following command to install the tool in your Kali Linux operating system.
git clone https://github.com/Cyber-Guy1/BlackDragon.git
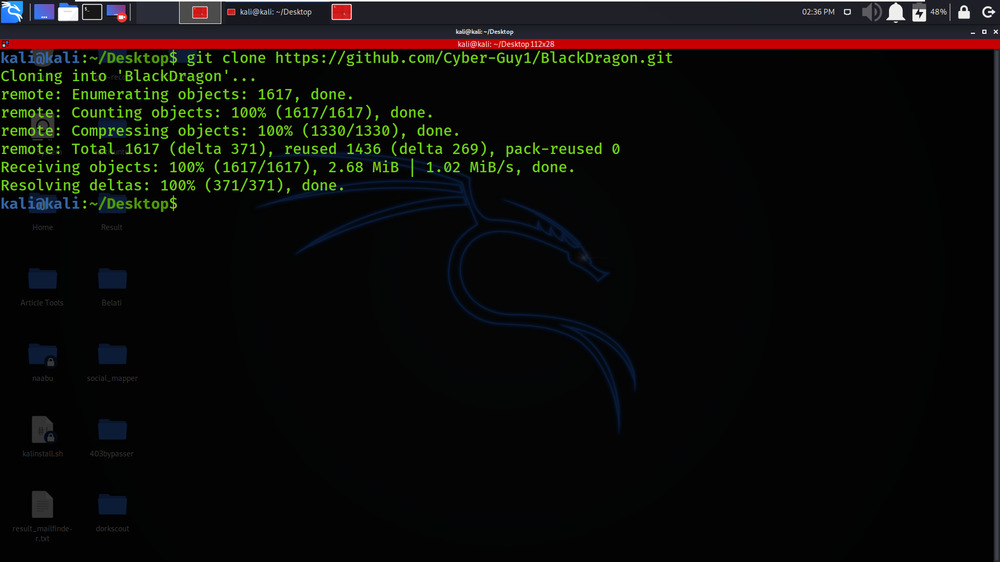
Step 2: Now use the following command to move into the directory of the tool. You have to move in the directory in order to run the tool.
cd BlackDragon
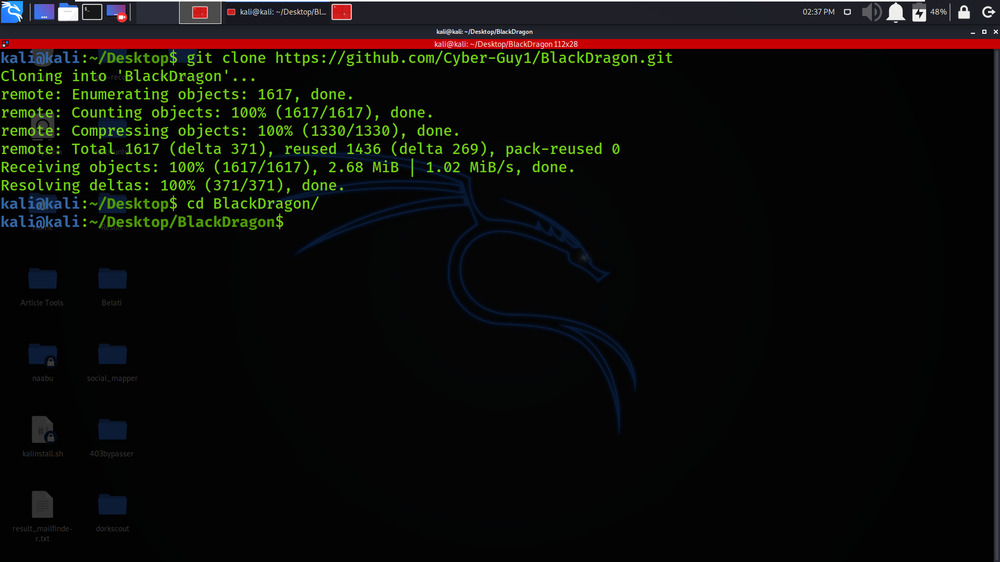
Step 3: Change the file permissions of the scripts as shown below.
sudo chmod +x install
sudo chmod +x Black-Dragon
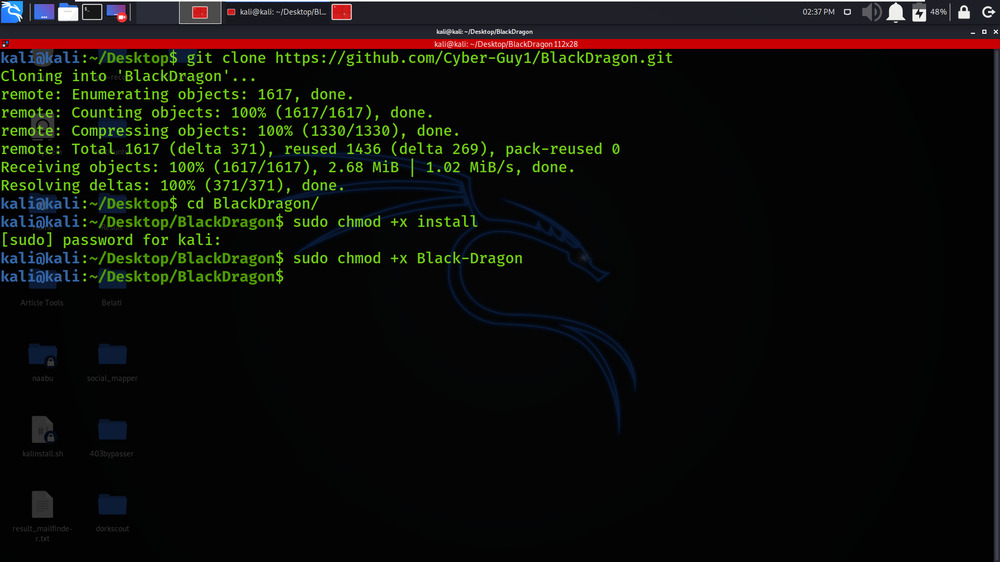
Step 4: Finally Run The Installation Script.
./install
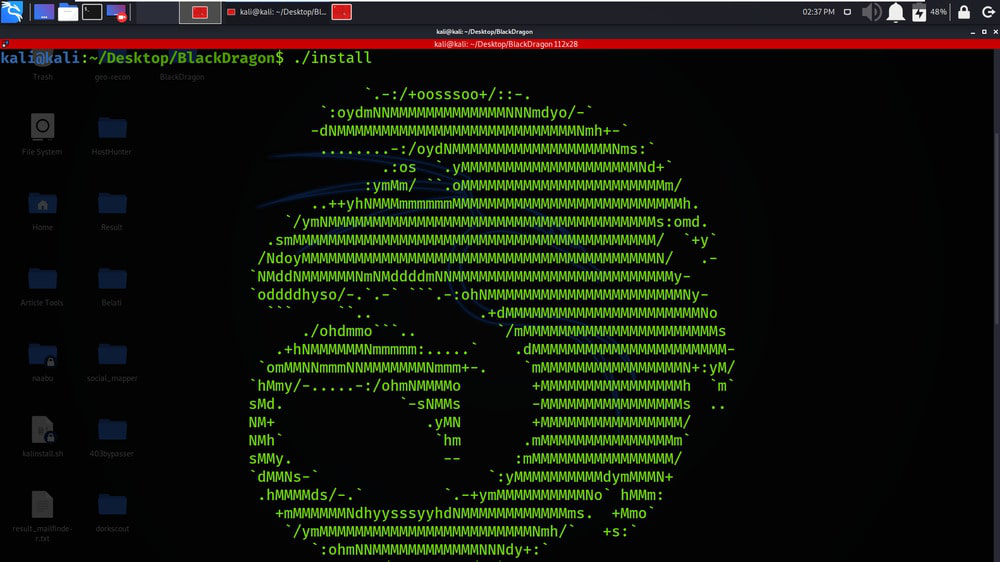
Step 5: Verify the installation using the following command.
./Black-Dragon
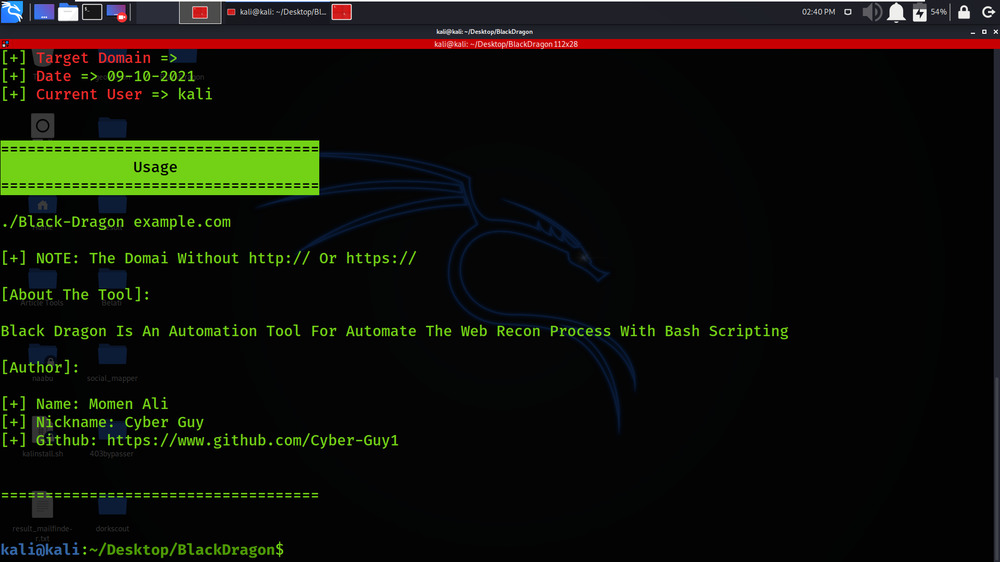
Working with BlackDragon Tool on Kali Linux OS
Example: Scanning geeksforgeeks.org domain
./Black-Dragon geeksforgeeks.org
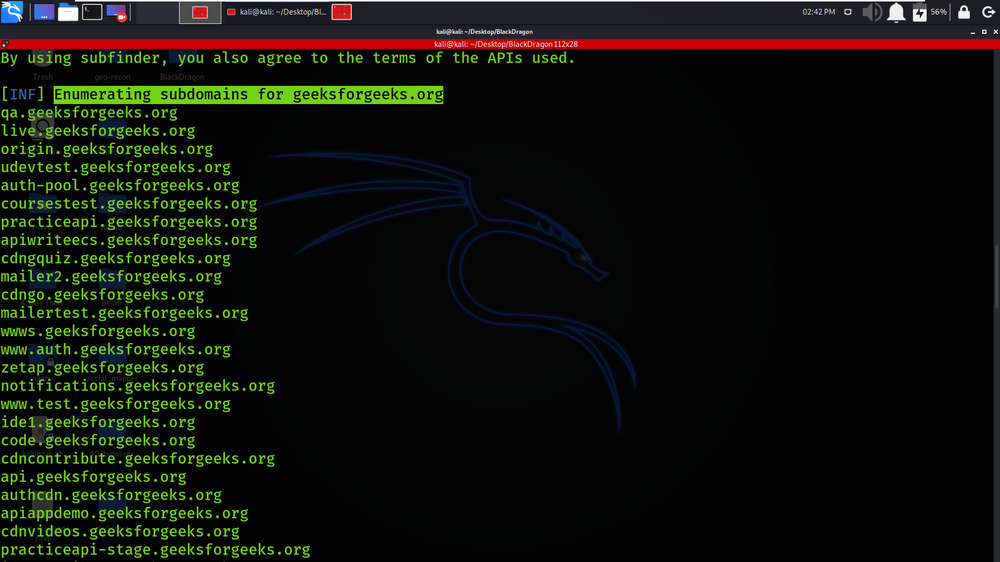
Subdomain Enumeration is performed using subfinder tool.
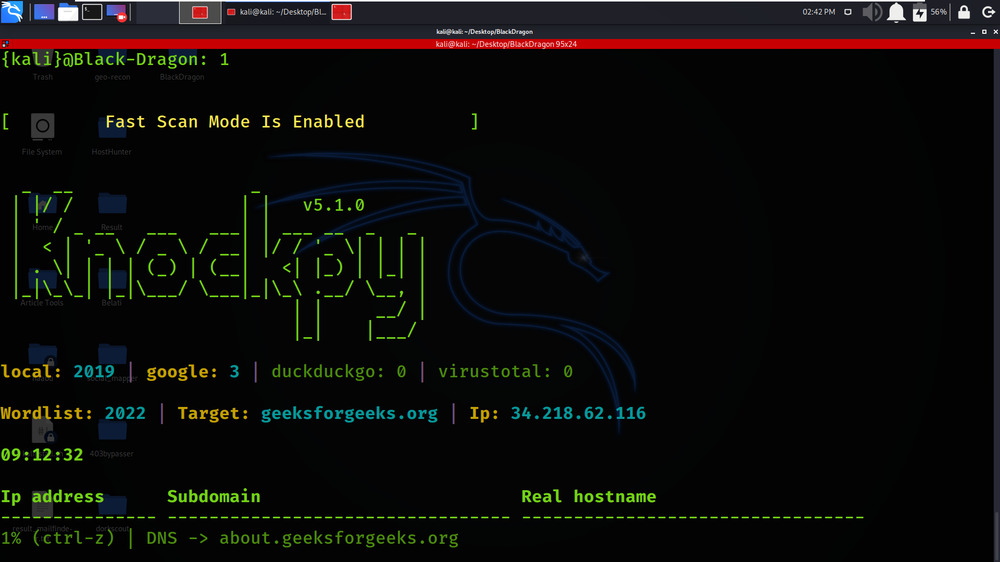
Fast Scan Mode is performed using the Knockpy tool.
Passive Recon is performed on geeksforgeeks.org using Amass tool.
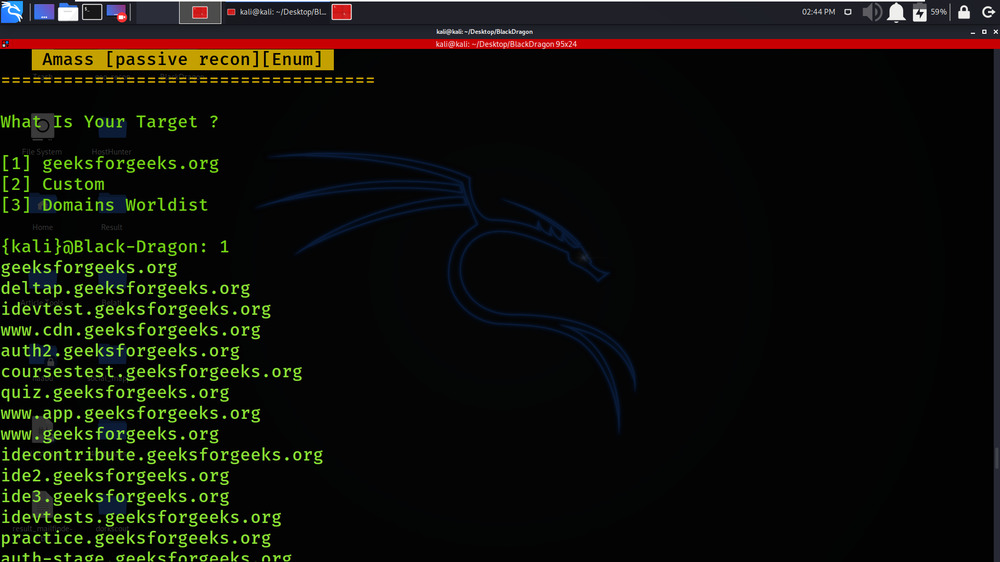
Active Recon is performed on geeksforgeeks.org using Amass tool.
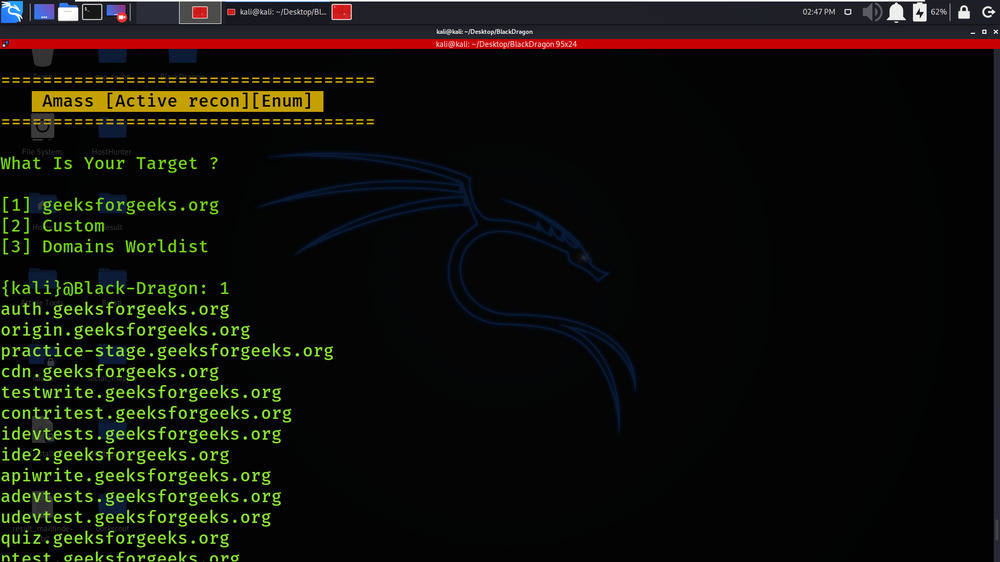
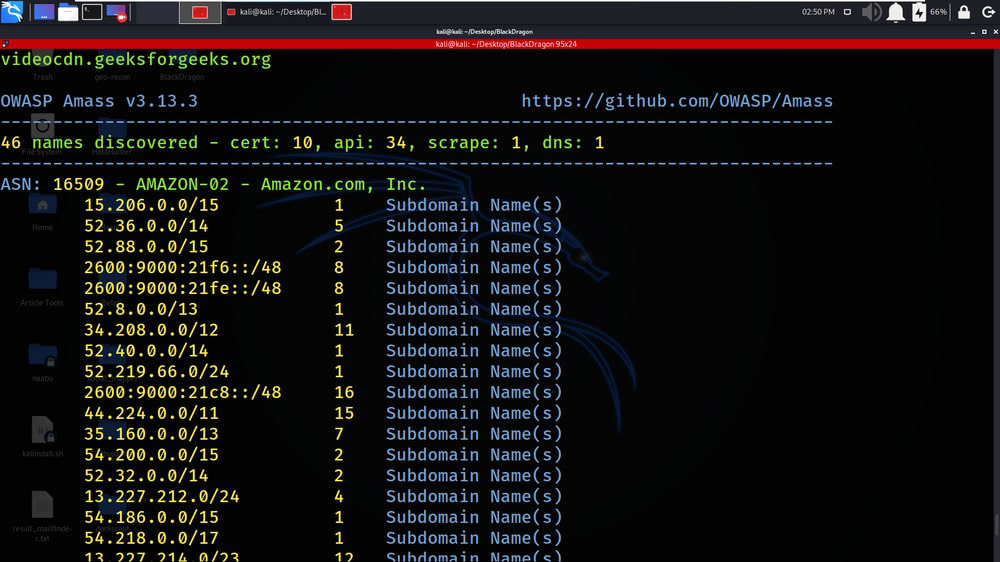
Results of Amass are shown in the below screenshot.
Share your thoughts in the comments
Please Login to comment...