Assign directions to edges so that the directed graph remains acyclic
Last Updated :
27 Jun, 2022
Given a graph with both directed and undirected edges. It is given that the directed edges don’t form cycle. How to assign directions to undirected edges so that the graph (with all directed edges) remains acyclic even after the assignment?
For example, in the below graph, blue edges don’t have directions.

We strongly recommend to minimize your browser and try this yourself first. The idea is to use Topological Sorting. Following are two steps used in the algorithm. 1) Consider the subgraph with directed edges only and find topological sorting of the subgraph. In the above example, topological sorting is {0, 5, 1, 2, 3, 4}.
Below diagram shows topological sorting for the above example graph.
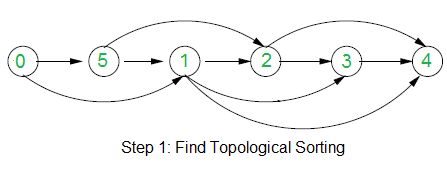
2) Use above topological sorting to assign directions to undirected edges. For every undirected edge (u, v), assign it direction from u to v if u comes before v in topological sorting, else assign it direction from v to u.
Below diagram shows assigned directions in the example graph.

Share your thoughts in the comments
Please Login to comment...