Program to compute Log n
Last Updated :
13 Sep, 2022
Write a one-line C function that calculates and returns 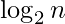 . For example, if n = 64, then your function should return 6, and if n = 128, then your function should return 7.
. For example, if n = 64, then your function should return 6, and if n = 128, then your function should return 7.
Using Recursion
C++
#include <iostream>
using namespace std;
unsigned int Log2n(unsigned int n)
{
return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
int main()
{
unsigned int n = 32;
cout << Log2n(n);
getchar();
return 0;
}
|
C
#include <stdio.h>
unsigned int Log2n(unsigned int n)
{
return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
int main()
{
unsigned int n = 32;
printf("%u", Log2n(n));
getchar();
return 0;
}
|
Java
class Gfg1
{
static int Log2n(int n)
{
return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
public static void main(String args[])
{
int n = 32;
System.out.println(Log2n(n));
}
}
|
Python3
def Log2n(n):
return 1 + Log2n(n / 2) if (n > 1) else 0
n = 32
print(Log2n(n))
|
C#
using System;
class GFG {
static int Log2n(int n)
{
return (n > 1) ? 1 +
Log2n(n / 2) : 0;
}
public static void Main()
{
int n = 32;
Console.Write(Log2n(n));
}
}
|
Javascript
<script>
function Log2n( n)
{
return (n > 1) ? 1 + Log2n(n / 2) : 0;
}
n = 32;
document.write( Log2n(n));
</script>
|
Output :
5
Time complexity: O(log n)
Auxiliary space: O(log n) if the stack size is considered during recursion otherwise O(1)
Using inbuilt log function
We can use the inbuilt function of the standard library which is available in the library.
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
unsigned int n = 32;
cout << (log(n) / log(2));
return 0;
}
|
C
#include <math.h>
#include <stdio.h>
int main()
{
unsigned int n = 32;
printf("%d", (int)log2(n));
return 0;
}
|
Java
import java.util.*;
class Gfg2
{
public static void main(String args[])
{
int n = 32;
System.out.println((int)(Math.log(n) / Math.log(2)));
}
}
|
Python3
import math
if __name__ == "__main__":
n = 32
print(int(math.log(n, 2)))
|
C#
using System;
class GFG{
static public void Main()
{
int n = 32;
Console.WriteLine((int)(Math.Log(n) / Math.Log(2)));
}
}
|
Javascript
<script>
n = 32;
document.write( Math.log2(n));
</script>
|
Output :
5
Time complexity: O(1)
Auxiliary space: O(1)
Let us try an extended version of the problem.
Write a one line function Logn(n, r) which returns 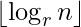 .
.
Using Recursion
C++
#include <bits/stdc++.h>
using namespace std;
unsigned int Logn(unsigned int n,
unsigned int r)
{
return (n > r - 1) ? 1 +
Logn(n / r, r) : 0;
}
int main()
{
unsigned int n = 256;
unsigned int r = 3;
cout << Logn(n, r);
return 0;
}
|
C
#include <stdio.h>
unsigned int Logn(unsigned int n, unsigned int r)
{
return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}
int main()
{
unsigned int n = 256;
unsigned int r = 3;
printf("%u", Logn(n, r));
return 0;
}
|
Java
class Gfg3
{
static int Logn(int n, int r)
{
return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}
public static void main(String args[])
{
int n = 256;
int r = 3;
System.out.println(Logn(n, r));
}
}
|
Python3
def Logn(n, r):
return 1 + Logn(n / r, r) if (n > r - 1) else 0
n = 256
r = 3
print(Logn(n, r))
|
C#
using System;
public class Gfg3
{
static int Logn(int n, int r)
{
return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}
public static void Main(String []args)
{
int n = 256;
int r = 3;
Console.WriteLine(Logn(n, r));
}
}
|
Javascript
<script>
function Logn( n, r)
{
return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}
n = 256;
r = 3;
document.write( Logn(n, r));
</script>
|
Output :
5
Time complexity: O(log n)
Auxiliary space: O(log n) if the stack size is considered during recursion otherwise O(1)
Using inbuilt log function
We only need to use the logarithm property to find the value of log(n) on arbitrary base r. i.e., 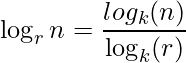 where k can be any anything, which for standard log functions are either e or 10
where k can be any anything, which for standard log functions are either e or 10
C++
#include <bits/stdc++.h>
using namespace std;
unsigned int Logn(unsigned int n,
unsigned int r)
{
return log(n) / log(r);
}
int main()
{
unsigned int n = 256;
unsigned int r = 3;
cout << Logn(n, r);
return 0;
}
|
C
#include <math.h>
#include <stdio.h>
unsigned int Logn(unsigned int n, unsigned int r)
{
return log(n) / log(r);
}
int main()
{
unsigned int n = 256;
unsigned int r = 3;
printf("%u", Logn(n, r));
return 0;
}
|
Java
import java.util.*;
class Gfg4 {
public static void main(String args[])
{
int n = 256;
int r = 3;
System.out.println((int)(Math.log(n) / Math.log(r)));
}
}
|
Python3
import math
def Logn(n, r):
return math.log(n) // math.log(r)
n = 256
r = 3
print(int(Logn(n, r)))
|
C#
using System;
class Gfg4 {
public static void Main(String []args)
{
int n = 256;
int r = 3;
Console.Write((int)(Math.Log(n) / Math.Log(r)));
}
}
|
Javascript
<script>
function Logn( n, r)
{
return Math.floor(Math.log(n) / Math.log(r));
}
n = 256;
r = 3;
document.write( Logn(n, r));
</script>
|
Output :
5
Time complexity: O(1)
Auxiliary space: O(1)
Share your thoughts in the comments
Please Login to comment...