Bubble Sort – Data Structure and Algorithm Tutorials
Last Updated :
12 Apr, 2024
Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity is quite high.
Bubble Sort Algorithm
In Bubble Sort algorithm,
- traverse from left and compare adjacent elements and the higher one is placed at right side.
- In this way, the largest element is moved to the rightmost end at first.
- This process is then continued to find the second largest and place it and so on until the data is sorted.
How does Bubble Sort Work?
Let us understand the working of bubble sort with the help of the following illustration:
Input: arr[] = {6, 0, 3, 5}
First Pass:
The largest element is placed in its correct position, i.e., the end of the array.
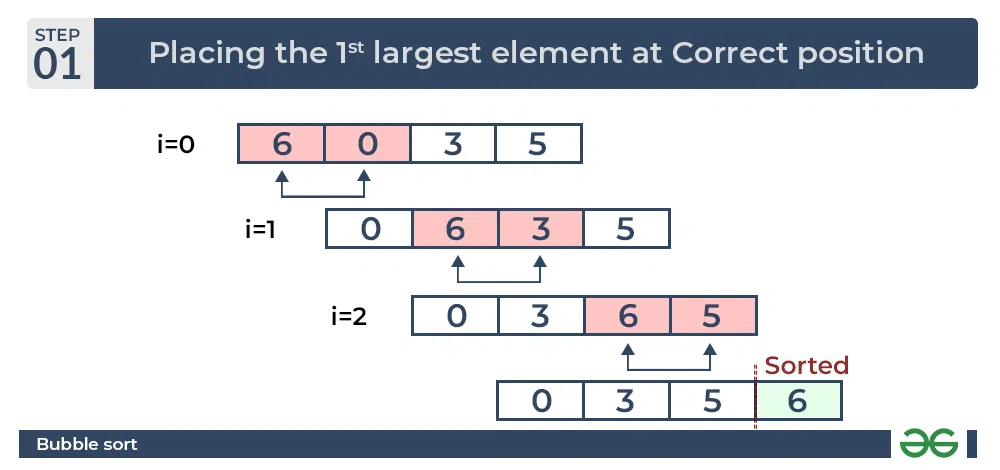
Bubble Sort Algorithm : Placing the largest element at correct position
Second Pass:
Place the second largest element at correct position
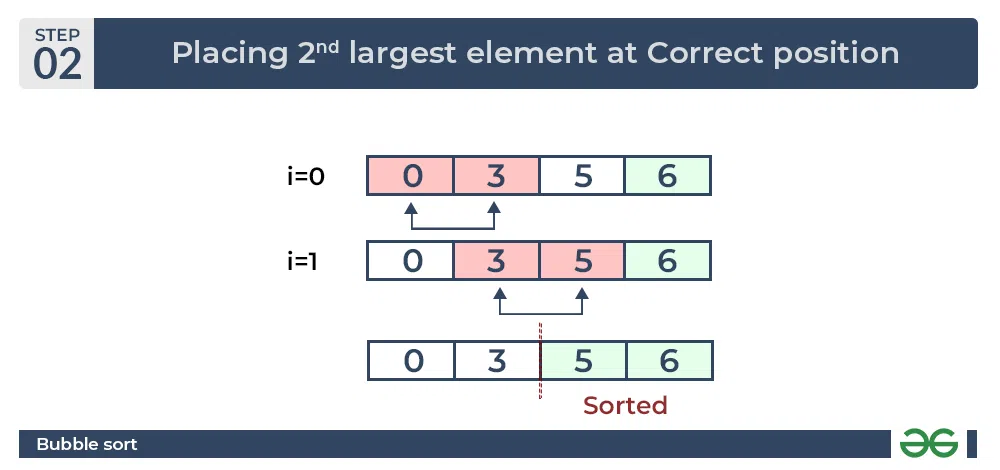
Bubble Sort Algorithm : Placing the second largest element at correct position
Third Pass:
Place the remaining two elements at their correct positions.
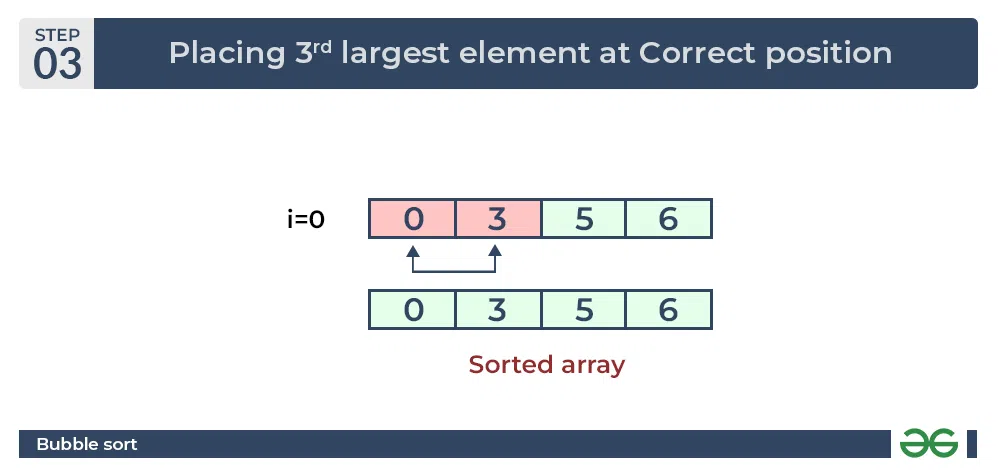
Bubble Sort Algorithm : Placing the remaining elements at their correct positions
- Total no. of passes: n-1
- Total no. of comparisons: n*(n-1)/2
Implementation of Bubble Sort
Below is the implementation of the bubble sort. It can be optimized by stopping the algorithm if the inner loop didn’t cause any swap.
C++
// Optimized implementation of Bubble sort
#include <bits/stdc++.h>
using namespace std;
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
swapped = true;
}
}
// If no two elements were swapped
// by inner loop, then break
if (swapped == false)
break;
}
}
// Function to print an array
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << " " << arr[i];
}
// Driver program to test above functions
int main()
{
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
int N = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, N);
cout << "Sorted array: \n";
printArray(arr, N);
return 0;
}
// This code is contributed by shivanisinghss2110
// Optimized implementation of Bubble sort
#include <stdbool.h>
#include <stdio.h>
void swap(int* xp, int* yp)
{
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(&arr[j], &arr[j + 1]);
swapped = true;
}
}
// If no two elements were swapped by inner loop,
// then break
if (swapped == false)
break;
}
}
// Function to print an array
void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
}
// Driver program to test above functions
int main()
{
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
int n = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr, n);
printf("Sorted array: \n");
printArray(arr, n);
return 0;
}
// Optimized java implementation of Bubble sort
import java.io.*;
class GFG {
// An optimized version of Bubble Sort
static void bubbleSort(int arr[], int n)
{
int i, j, temp;
boolean swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap arr[j] and arr[j+1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// If no two elements were
// swapped by inner loop, then break
if (swapped == false)
break;
}
}
// Function to print an array
static void printArray(int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
// Driver program
public static void main(String args[])
{
int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
int n = arr.length;
bubbleSort(arr, n);
System.out.println("Sorted array: ");
printArray(arr, n);
}
}
// This code is contributed
// by Nikita Tiwari.
# Optimized Python program for implementation of Bubble Sort
def bubbleSort(arr):
n = len(arr)
# Traverse through all array elements
for i in range(n):
swapped = False
# Last i elements are already in place
for j in range(0, n-i-1):
# Traverse the array from 0 to n-i-1
# Swap if the element found is greater
# than the next element
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
swapped = True
if (swapped == False):
break
# Driver code to test above
if __name__ == "__main__":
arr = [64, 34, 25, 12, 22, 11, 90]
bubbleSort(arr)
print("Sorted array:")
for i in range(len(arr)):
print("%d" % arr[i], end=" ")
# This code is modified by Suraj krushna Yadav
// Optimized C# implementation of Bubble sort
using System;
class GFG {
// An optimized version of Bubble Sort
static void bubbleSort(int[] arr, int n)
{
int i, j, temp;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
// Swap arr[j] and arr[j+1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// If no two elements were
// swapped by inner loop, then break
if (swapped == false)
break;
}
}
// Function to print an array
static void printArray(int[] arr, int size)
{
int i;
for (i = 0; i < size; i++)
Console.Write(arr[i] + " ");
Console.WriteLine();
}
// Driver method
public static void Main()
{
int[] arr = { 64, 34, 25, 12, 22, 11, 90 };
int n = arr.Length;
bubbleSort(arr, n);
Console.WriteLine("Sorted array:");
printArray(arr, n);
}
}
// This code is contributed by Sam007
// Optimized javaScript implementation
// of Bubble sort
// An optimized version of Bubble Sort
function bubbleSort(arr, n)
{
var i, j, temp;
var swapped;
for (i = 0; i < n - 1; i++)
{
swapped = false;
for (j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
// Swap arr[j] and arr[j+1]
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
// IF no two elements were
// swapped by inner loop, then break
if (swapped == false)
break;
}
}
// Function to print an array
function printArray(arr, size)
{
var i;
for (i = 0; i < size; i++)
console.log(arr[i] + " ");
}
// Driver program
var arr = [ 64, 34, 25, 12, 22, 11, 90 ];
var n = arr.length;
bubbleSort(arr, n);
console.log("Sorted array: ");
printArray(arr, n);
// This code is contributed shivanisinghss2110
<?php
// PHP Optimized implementation
// of Bubble sort
// An optimized version of Bubble Sort
function bubbleSort(&$arr)
{
$n = sizeof($arr);
// Traverse through all array elements
for($i = 0; $i < $n; $i++)
{
$swapped = False;
// Last i elements are already
// in place
for ($j = 0; $j < $n - $i - 1; $j++)
{
// Traverse the array from 0 to
// n-i-1. Swap if the element
// found is greater than the
// next element
if ($arr[$j] > $arr[$j+1])
{
$t = $arr[$j];
$arr[$j] = $arr[$j+1];
$arr[$j+1] = $t;
$swapped = True;
}
}
// If no two elements were swapped
// by inner loop, then break
if ($swapped == False)
break;
}
}
// Driver code
$arr = array(64, 34, 25, 12, 22, 11, 90);
$len = sizeof($arr);
bubbleSort($arr);
echo "Sorted array: \n";
for($i = 0; $i < $len; $i++)
echo $arr[$i]." ";
// This code is contributed by ChitraNayal.
?>
OutputSorted array:
11 12 22 25 34 64 90
Time Complexity: O(N2)
Auxiliary Space: O(1)
Advantages of Bubble Sort:
- Bubble sort is easy to understand and implement.
- It does not require any additional memory space.
- It is a stable sorting algorithm, meaning that elements with the same key value maintain their relative order in the sorted output.
Disadvantages of Bubble Sort:
- Bubble sort has a time complexity of O(N2) which makes it very slow for large data sets.
- Bubble sort is a comparison-based sorting algorithm, which means that it requires a comparison operator to determine the relative order of elements in the input data set. It can limit the efficiency of the algorithm in certain cases.
Some FAQs related to Bubble Sort:
What is the Boundary Case for Bubble sort?
Bubble sort takes minimum time (Order of n) when elements are already sorted. Hence it is best to check if the array is already sorted or not beforehand, to avoid O(N2) time complexity.
Does sorting happen in place in Bubble sort?
Yes, Bubble sort performs the swapping of adjacent pairs without the use of any major data structure. Hence Bubble sort algorithm is an in-place algorithm.
Is the Bubble sort algorithm stable?
Yes, the bubble sort algorithm is stable.
Where is the Bubble sort algorithm used?
Due to its simplicity, bubble sort is often used to introduce the concept of a sorting algorithm. In computer graphics, it is popular for its capability to detect a tiny error (like a swap of just two elements) in almost-sorted arrays and fix it with just linear complexity (2n).
Example: It is used in a polygon filling algorithm, where bounding lines are sorted by their x coordinate at a specific scan line (a line parallel to the x-axis), and with incrementing y their order changes (two elements are swapped) only at intersections of two lines.
Related Articles:
Share your thoughts in the comments
Please Login to comment...