What is Gibbs Sampling?

Last Updated : 09 Dec, 2023

In statistics and machine learning, Gibbs Sampling is a potent Markov Chain Monte Carlo (MCMC) technique that is frequently utilized for sampling from intricate, high-dimensional probability distributions. The foundational ideas, mathematical formulas, and algorithm of Gibbs Sampling are examined in this article.

Gibbs Sampling

Gibbs sampling is a type of Markov Chain Monte Carlo(MCMC) method in which we sample from a set of multivariate(having different variables) probability distributions, it is typically considered to be difficult to sample joint distribution from the multivariate distribution so we consider conditional probability. Instead of calculating joint probability p(x₁, x₂, x₃…..x_n), we will be calculating conditionals p(x_i|x₂, x₃….x_n) for every variable. The concept behind Gibbs Sampling is that we can update the value of variable x_i keeping other variables having the current value. The process of updating variables and keeping others fixed creates a Markov Chain, after several iterations the chain converges to the joint distribution. Rather than finding the sample from joint distribution, we will prefer to find samples from conditional distribution for multivariate probability distribution which then tends to give us the joint distribution sampling.

Markov Chain Monte Carlo Method

Let’s discuss about Markov Chain Monte Carlo(MCMC) method in a little detail so that we can get intuition about the Gibbs Sampling.

In a Markov Chain, the future state depends on the current state and is independent of the previous state. To get a sample from the joint distribution, a Markov chain is created such that its stationary state corresponds to the target distribution. Until the stationary state is reached the samples taken into account are considered to be burn in state.

Monte Carlo methods corresponds to the random sampling of distribution when direct sampling from the distribution is not feasible.

In MCMC a random sample chain is formed X_i -> X_i+1 with the help of transition probability(T(X_i+1|X_i)) which is actually the probability that the sample state X_i will switch to X_i+1 which is an implication that X_i+1 marks higher density than X_i in the p(x). We need to iterate over the process of switching from one sample to another until a series of stationary samples are obtained which tells us about the final state of samples, after this state the samples are not going to change and we can even match the stationary state with the target sample.

Let’s say that we start the sampling from X₀, therefore the sampling process goes on like a chain – X₀ -> X₁ -> X₂ -> ………. X_m -> X_m -> X_m+2 -> …and so on.

Here lets say that the samples starts matching the target distribution from X_m, so the steps taken to reach X_m form X₁ to X_m-1 is considered to be burn in phase. The burn in phase is required to reach the required target samples.

The stationary state is reached when the distribution satisfies the equation =

$\Sigma p(x) * T(y|x) = \Sigma p(y) * T(x|y)$

where T(y|x) is the transition probability from y -> x and T(x|y) is the transition probability from x -> y

For the sake of simplicity let us consider the distribution is among three variables X, Y, Z and we want to sample joint distribution p(X, Y, Z).

Gibbs Sampling Algorithm

First initialize each variable present in the system by assigning values to them.
Then select any variable from the system X_i, the selection choice of variable is not important.
Now sample a new value of X_i from the conditional distribution given other variables are the same p(X_i|X₁, X₂,…,X_i-1,X_i+1,……X_n) and update the value of X_i in the sample.
Repeat the iteration for a number of iterations with one variable at a time and for all the variables present in the system.
A Markov Chain is created in the process which converges to the target distribution, we have to discard the initial values which led us to the target sample i.e. we have to discard the burn in phase.

Psuedocode for Gibbs Sampling Algorithm

Initialize variables randomly or with some initial values
for each iteration t do:
    for each variable i do:
        Sample x_i from P(x_i | x_1, x_2, ..., x_{i-1}, x_{i+1}, ..., x_n)
        Update x_i in the current state
The above process is repeated for a sufficient number of iterations to allow the chain to converge to the target distribution.

The variables are initialized either randomly or with predetermined beginning values at the start of the Gibbs Sampling process. After that, iteratively cycling through each variable, it updates its value according to the conditional distribution based on how the other variables are currently doing. Taking into account the values of the nearby variables, a sample is taken from the conditional distribution of each variable x_i. The current state is then updated using this sampled value. After a significant number of repetitions, the Markov chain is able to explore the joint distribution and eventually converge to the target distribution. This procedure is repeated. High-dimensional probability spaces can be effectively navigated by Gibbs Sampling due to its sequential variable update and dependence on conditional distributions.

Gibbs Sampling Function

Gibbs sampling involves various mathematical functions and expressions. Here are some common ones:

Conditional Probability: We can express the conditional probability as P(x | y) , we use the vertical bar (|) within a fraction: [ P(x | y) ]
Gaussian Distribution: We can use the $\Nu$ symbol to represent the Gaussian distribution (normal distribution). The parameters (mean and variance) can be specified in subscript and superscript: [ $\Nu(\mu, \sigma^2)$ ]
Summation: We can represent a summation, we can use the 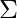$\Sigma$ symbol: $[\Sigma _{i=1} ^n x_i]$ This example represents the sum of x subscripts from 1 to n.
Random variables: We can represent random variables as [X, Y, Z].
Mean and variance: 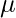$\mu$ is used to represent mean whereas $\sigma^2$ is used to represent variance, [ $\mu, \sigma^2$ ]

Therefore the conditional probability of x given y can be represented using gaussian distribution using mean(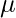 $\mu$ ) and variance( $\sigma^2$ ) as:

P(x |y) = $\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}$

Steps to implement Gibbs Sampling Algorithm

First we need to understand the problem and know the conditional probability of the variables we need to sample. Let’s say we have three variables X, Y, Z and we want to find their joint probability.
After that we need to consider initial values for X, Y and Z, let’s say they are X₀, Y₀, Z₀.
Now we find the value of X keeping the value of Y and Z constant as the current values and randomly decide if we should change the value of X to the new value or the initial value, if we decide to take the new value we must update X from X₀ to X₁.
In the same way we find the value of Y keeping the value of X and Z constant as the current values and randomly decide if we should change the value of Y to the new value or the initial value, if we decide to take the new value we must update Y from Y₀ to Y₁.
Again we find the value of Z keeping the value of X and Y constant as the current values and randomly decide if we should change the value of Z to the new value or the initial value, if we decide to take the new value we must update Z from Z₀ to Z₁.
We keep repeating the third, fourth and the fifth steps to get new values of X, Y, Z and store their set (X_i, Y_j, Z_k) which will correspond to new samples.
After a period the samples stored will converge to the target joint probability, we must consider recording the start of the joint probability and ignore the steps which were required to reach that distribution as those steps are considered to be burn in phase.

We can repeat what we just did with 3 variable distribution with ‘n’ variable distribution keeping ‘n-1’ variables constant.

Example of Gibbs sampling

Suppose we have two variables(X, Y) which takes two values 0 and 1, we want to sample from their joint distribution p(X, Y) which is defined as follows:

p(X=0, Y=0) = 0.2

p(X=1, Y=0) = 0.3

p(X=0, Y=1) = 0.1

p(X=1, Y=1) = 0.4

Let’s follow the above instructions to find out the join probability:

Initialize X and Y, let’s say X=0 and Y=0

p(X=0|Y=0) = p(X=0,Y=0)/p(Y=0) = 0.2 / (0.3 + 0.2) = 0.4
p(X=1|Y=0) = 1 – p(X=0, Y=0) = 1 – 0.4 = 0.6

We can see that the p(X=1|Y=0) > p(X=0|Y=0), therefore let’s consider X = 1

p(Y=0|X=1) = 0.3 / (0.3 + 0.4) = 0.429
p(Y=1|X=1) = 0.4 / (0.3 + 0.4) = 0.571

We can see that the p(Y=1|X=1) > p(Y=0|X=1), therefore let’s consider Y = 1

Now we get new sample (X = 1, Y = 1) from initial (X = 0, Y = 0) sample.

Implementation of Gibbs Sampling

Lets use real world dataset to perform Gibbs sampling on it, for this example we will be using iris flower dataset which has 4 features namely Sepal Length in cm, Sepal Width in cm, Petal Length in cm, Petal Width in cm and a target column named “Species” which specifies which specie of flower the given flower information belongs to. We will be using three features out of the features column and sampling from them, the three features that we are going to consider are Sepal Length in cm, Sepal Width in cm and Petal Length in cm and we will be sampling using Gibbs sampling. Now that we have the knowledge about the dataset lets sample from it to get more insightful and concrete knowledge about Gibbs Sampling. The link to get the iris dataset is present here – link.

Python3

# code
# importing libraries
import random
import pandas as pd
import numpy as np
 
# Load the Iris dataset into pandas
df = pd.read_csv("Iris.csv", index_col=0)
 
# This dataframe contains the sepal length, sepal width and petal length features
data_pd = df.drop(["Species", "PetalWidthCm"], axis=1)
data = data_pd.to_numpy()
 
 
# Initial values for sepal length, sepal width and petal length
initial_x = random.uniform(min(data[:, 0]), max(data[:, 0]))
initial_y = random.uniform(min(data[:, 1]), max(data[:, 1]))
initial_z = random.uniform(min(data[:, 2]), max(data[:, 2]))
 
# Number of Gibbs sampling iterations
num_iterations = 20
samples = []
 
for _ in range(num_iterations):
    # Sample sepal length (x) from the conditional distribution P(x | y, z)
    x_mean = sum(data[:, 0]) - initial_x
    x = random.gauss(x_mean, 1)
 
    # Sample sepal width (y) from the conditional distribution P(y | x, z)
    y_mean = sum(data[:, 1]) - initial_y
    y = random.gauss(y_mean, 1)
 
    # Sample petal length (z) from the conditional distribution P(z | x, y)
    z_mean = sum(data[:, 2]) - initial_z
    z = random.gauss(z_mean, 1)
 
    samples.append((x, y, z))
 
# Printing the final samples
samples

Output:

[(872.4402040624939, 455.07624627880733, 557.1998684063759),
 (873.1969054020584, 455.1091251130041, 557.2860844837276),
 (873.3693504710424, 453.18776626786007, 556.3740798243281),
 (873.083812669017, 455.72828252467434, 557.668346144098),
 (870.276168841318, 455.4399496509379, 558.3048356159429),
 (874.106506516945, 454.29506297022715, 556.1389162989519),
 (872.1696929984183, 455.5786052550156, 555.8268260569116),
 (872.9197678225382, 453.47746463366445, 559.2402273152256),
 (872.7355987922335, 455.11858023950083, 558.5099559019588),
 (872.3610146956339, 457.40524015004314, 557.8652047189928),
 (871.8045749612949, 456.44003748102057, 555.2727928873985),
 (871.0080667027727, 455.472656507735, 556.2694177512999),
 (872.8301827815144, 457.9253456275969, 557.9428716857147),
 (873.5047861748837, 456.4206214302957, 556.1488817783928),
 (871.4013471768071, 452.929785672875, 558.4311648765539),
 (873.1824338211024, 456.59460170394635, 556.7295027720941),
 (871.6812463694724, 454.59545177891346, 557.0859288787802),
 (872.2302391176851, 452.64086443804536, 557.0920231397946),
 (871.8371328846458, 457.07248956342806, 558.2378397896033),
 (872.3803212658619, 455.49860327871284, 558.0196097954986)]

Here in this code we imported three libraries named random to generate random numbers, pandas to manipulate data and we used and alias as ‘pd’ for it and numpy to compute numerical operations and again we used an alias as ‘np’. After that we read the csv file named ‘Iris.csv’ which is provided above and stored it into a variable named df. Then we prepared our data for gibbs sampling by dropping the columns ‘Species’ and ‘PetalWidthCm’ from the dataframe by using the method Dataframe.drop() and stored the remaining dataframe into a variable named data_pd, we did this since we will be sampling from three features named ‘SepalLengthCm’, ‘SepalWidthCm’ and ‘PetalLengthCm’. After this step we converted the data_pd into numpy array by using .to_numpy() method, which converted data_pd into a numpy matrix.

After following the above steps we started to get to the Gibbs Sampling part of the code, first we initialized three variables initial_x, initial_y, initial_z randomly from the range of values of the three features respectively. Then we assigned value to num_iterations variable that is how many samples that are going to be generated and it is set to 20, the stage to apply Gibbs Sampling has come so we iterate num_iterations time taking conditional of the three variables one at a time and changing the mean to new mean with standard deviation equals one and assigning new values to variables from random gauss distribution to get the samples.

Finally we will be appending all the samples to an empty list named ‘samples’ and printing it.

Advantages and Disadvantages of Gibbs Sampling

Advantages

Gibbs Sampling is relatively easy to implement if we compare it with other MCMC methods like Metrapolis-Hastings since it requires straightforward conditional distribution.
Proposals are always accepted in Gibbs Sampling unlike Metrapolis-Hastings where accept-reject proposals happen.
With the knowledge of conditional distribution of variables we can easily get the joint distribution of all the variables, which might get complex if we try direct method.

Disadvantages

Gibbs Sampling may not be useful in case of complex distribution with irregular shapes where conditional distributions are difficult to obtain.
It can be very slow in convergence if the variables are highly correlated.
Conditional dependencies becomes complex if there are higher dimensions resulting in inaccuracy.

Suggest improvement

What is Upsampling in MATLAB?

Share your thoughts in the comments