Box plot is basically an interval scale that is used to perform estimation which necessarily performs the abstraction of the data. Boxplots are used to interpret and analyze the data. It can also be used to visualize the data. Boxplot is a variation of the graphical method which is used to illustrate the variation of the data in the data distribution. A histogram can also be used in order to display the data. However, if we compare a box plot and histogram, the latter offers a sufficient display. It also provides additional information corresponding to the multiple sets of data which is displayed in the same graph.
Box plots can necessarily be used in situations when:
- Distribution Shape
- Central Value
- Variability
Upon plotting a graph for the box plot, a box starting from the first quartile to the third quartile is outlined. A vertical line that goes through this plotted box corresponds to the median of the data distribution. The small lines, called the whiskers go from each of the quartiles towards the minimum or maximum value. This concept is shown in the below figure:

Features of Box Plot
- It exhibits data from a five-number summary, which is also inclusive of one of the measures of central tendency. This implies that it has five pieces of information.
- Particularly used to reflect if the dataset given is a skewed distribution or not.
- It also provides an insight into the data set, that whether there is potential unusual observation. These are called outliers.
- It reflects information about how the data is spread out.
- Herein, the arrangements can be matched with each other. This is because, the center, spread, and overall range are instantly apparent in the case of a box plot.
- It is particularly useful for descriptive data interpretation.
- It is also used where huge numbers of data collections are involved or compared.
Elements of a Box and Whisker Plot
The elements required to construct a box and whisker plot outliers are given below:
Minimum value (Q0 or 0th percentile): The minimum specified value in the given dataset distribution, shown at the leftmost end.
First quartile (Q1 or 25th percentile): The first quartile (Q1) at the left side, which corresponds to the area in between the minimum value and median.
Median (Q2 or 50th percentile): The median value, depicted by the line corresponding to the center of the box.
Third quartile (Q3 or 75th percentile): The third quartile (Q3) at the right side, which corresponds to the area in between the median and the maximum value.
Maximum value (Q4 or 100th percentile): The maximum specified value in the given dataset distribution, shown at the rightmost end.
Interquartile range: Interquartile range (IQR) is the difference between upper and lower quartiles, i.e. Q3 and Q1.
Constructing a Box Plot?
The box and whiskers plot can be constructed using the following steps:
- The smallest value in the specified dataset is known as the minimum value.
- The value that corresponds to below the lower 25% of the contained data. It is called the first quartile.
- The third value corresponds to the median of the given data.
- The value that corresponds to above the lower 25% of the contained data. It is called the third quartile.
- The largest value in the specified dataset is known as the maximum value.
Applications
The box plot can be used to know the following components:
- The outliers and their values
- Tight grouping of data
- Symmetry of Data
- Data skewness
Sample Questions
Question 1. Calculate the
- Maximum value,
- Minimum value,
- Median,
- First quartile,
- Third quartile
From this given data:
2, 7, 19, 12, 23, 15, 26.
Solution:
First arrange this data in ascending order.
2, 7, 12, 15, 19, 23, 26
Hence here,
- Minimum value = 2
- Maximum value = 26
- Median =
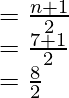
Median = 4th term = 15 - First Quartile = Middle value of 2, 7, 19
That is 7
Thus First Quartile = 7 - Third Quartile = Middle value of 19, 23, 26
That is 23
Thus Third Quartile = 23
Question 2. Draw the box plot for the given data:
2, 17, 20, 5, 3, 13, 15, 9, 11
Solution:
First arrange this data in ascending order
2, 3, 5, 9, 11, 13, 15, 17, 20
Find the Range of the data
Range = Maximum value in this data – Minimum value in this data
Range = 20 – 2 = 18
Now,
Find the Median
Median = 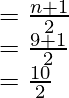
Median = 5th term
Median = 11
Further,
Find the quartiles.
Finding the First quartile (Q1) = The first quartile (Q1) at the left side, which is in between the minimum value and median.
Q1 = Median of (2, 3, 5, 9)
Q1 = 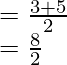
Q1 = 4
Now,
Finding the Third quartile (Q3) = The third quartile (Q3) at the right side, which is in between the median and the maximum value.
Q3 = Median of (13, 15, 17, 20)
Q3 = 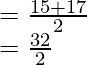
Q3 = 16
Thus,
Finding the interquartile range;
Interquartile = Q3 – Q1 = 16 – 4 = 12
Thus the five-number summary can be shown as:
Minimum value, First quartile Q1, Median, Third quartile Q3, Maximum value
Therefore,
2, 4, 11, 16, 20
Thus this is the five-number summary of the given data.
Hence,
Box plot can be drawn

Question 3. Mention the advantages of Box Plot
Solution:
The box and whisker plot has the following advantages :
Easy identification of the data location and data spread.
Information about the skewness and symmetry of data.
Information about the data outliers.
Question 4. Mention the disadvantages of Box Plot
Solution:
The box and whisker plot has the following disadvantages :
Mean cannot be easily located.
It generally hides the multimodality and other characteristics of given distributions.
Question 5. Calculate the
- Maximum value,
- Minimum value,
- Median,
- First quartile,
- Third quartile
From this given data:
5, 7, 2, 19, 25, 18, 26, 9, 11.
Solution:
First arrange this data in ascending order.
2, 5, 7, 9, 11, 18, 19, 25, 26
Hence here,
Minimum value = 2
Maximum value = 26
Median = 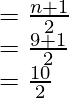
Median = 5th term = 11
First Quartile = Middle value of 2, 5, 7, 9
That is 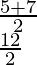
Thus First Quartile = 6
Third Quartile = Middle value of 18, 19, 25, 26
That is 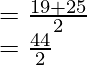
Thus Third Quartile = 22.
Share your thoughts in the comments
Please Login to comment...