Rotate Image by 90 degree

Given an image represented by n*m matrix, rotate the image by 90 degrees in clockwise direction.

Matrix: 1  2  3
               4  5  6
               7  8  9

Output:  7  4  1
              8  5 2
              9  6  3

Input:

Matrix: 1  2  3  4 
               5  6  7  8 
               9 10 11 12 

Output:  9  5  1 
               10  6 2 
               11  7 3
              12  8  4 

In pictorial form, we can represent the transformations of an (n x m) matrix into (m x n) matrix,

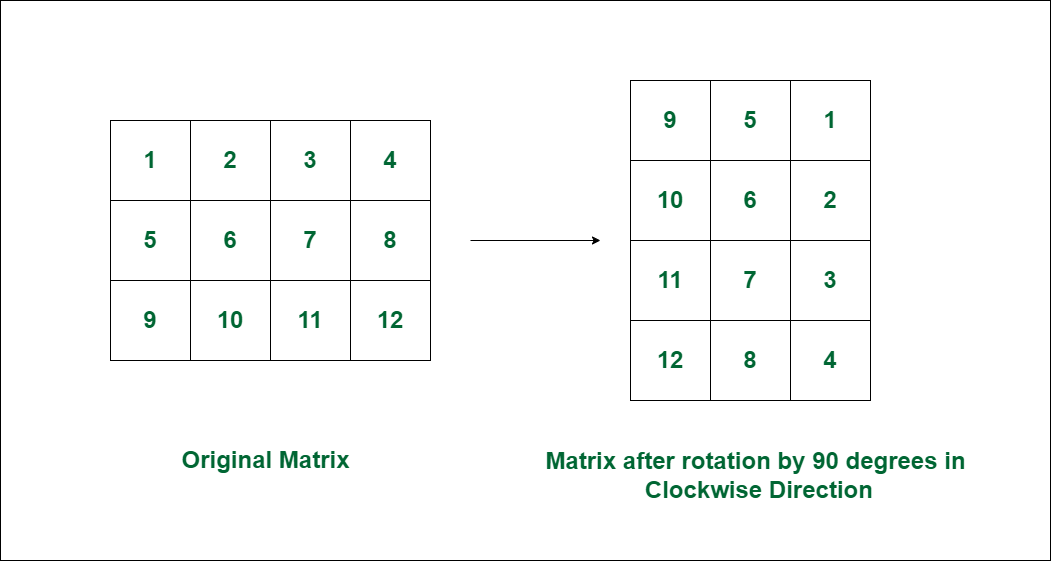
Rotate Image

Approach:

Transform each row of original matrix into required column of final matrix. From the above picture, we can observe that:

first row of original matrix——> last column of final matrix

second row of original matrix——> second last column of final matrix

so on …… last row of original matrix——> first column of final matrix

Follow the steps to implement the idea:

• Create a new matrix to hold the rotated image containing m rows and n columns.
• For each element at position (i, j) in the original matrix, its new position will be(j, n - 1 - i) will be in rotated matrix ( the rows are flipped when transferring to the columns of the new matrix).
• Make original matrix equal to the new matrix, which is the matrix after rotation by 90 degrees in clockwise direction.

Below is the implementation of above approach

C++

// C++ program to rotate a matrix
// by 90 degrees
#include <bits/stdc++.h>

using namespace std;

// Function to
// rotate a N x M matrix
// by 90 degrees in
// clockwise direction
void rotateMatrix(vector<vector<int> >& mat)
{
    int n = mat.size();
    int m = mat[0].size();
    vector<vector<int> > new_mat(m, vector<int>(n));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            new_mat[j][n - i - 1] = mat[i][j];
        }
    }
    mat = new_mat;
}

// Function to print the matrix
void displayMatrix(vector<vector<int> >& mat)
{
    int n = mat.size();
    int m = mat[0].size();
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cout << mat[i][j] << " ";
        }
        cout << endl;
    }
    cout << endl;
}

/* Driver code */
int main()
{
    // Test Case 1
    vector<vector<int> > mat{
        { 1, 2, 3, 4 },
        { 5, 6, 7, 8 },
        { 9, 10, 11, 12 },
    };

    // Function call
    rotateMatrix(mat);

    // Print rotated matrix
    displayMatrix(mat);

    return 0;
}

Java

public class MatrixRotation {
    // Function to rotate a N x M matrix by 90 degrees in clockwise direction
    static void rotateMatrix(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        int[][] newMat = new int[m][n];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                newMat[j][n - i - 1] = mat[i][j];
            }
        }

        // Copy the rotated matrix back to the original matrix
        mat = newMat;
    }

    // Function to print the matrix
    static void displayMatrix(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                System.out.print(mat[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        // Test Case 1
        int[][] mat = {
            {1, 2, 3, 4},
            {5, 6, 7, 8},
            {9, 10, 11, 12}
        };

        // Function call to rotate the matrix
        rotateMatrix(mat);

        // Print the rotated matrix
        displayMatrix(mat);
    }
}

Python3

# Function to rotate a N x M matrix by 90 degrees in clockwise direction
def rotateMatrix(mat):
    n = len(mat)
    m = len(mat[0])
    new_mat = [[0] * n for _ in range(m)]
    for i in range(n):
        for j in range(m):
            new_mat[j][n - i - 1] = mat[i][j]
    return new_mat

# Function to print the matrix
def displayMatrix(mat):
    n = len(mat)
    m = len(mat[0])
    for i in range(n):
        for j in range(m):
            print(mat[i][j], end=" ")
        print()
    print()

# Driver code
if __name__ == "__main__":
    # Test Case 1
    mat = [
        [1, 2, 3, 4],
        [5, 6, 7, 8],
        [9, 10, 11, 12],
    ]

    # Function call to rotate matrix
    mat = rotateMatrix(mat)

    # Print rotated matrix
    displayMatrix(mat)

C#

using System;
using System.Collections.Generic;

class Program
{
    // Function to rotate a matrix by 90 degrees clockwise
    static void RotateMatrix(List<List<int>> mat)
    {
        int n = mat.Count;      // Number of rows in the original matrix
        int m = mat[0].Count;   // Number of columns in the original matrix

        // Create a new matrix with dimensions swapped (m x n)
        List<List<int>> newMat = new List<List<int>>();
        for (int i = 0; i < m; i++)
        {
            newMat.Add(new List<int>());
            for (int j = 0; j < n; j++)
            {
                newMat[i].Add(0);
            }
        }

        // Fill the new matrix with rotated values
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                newMat[j][n - i - 1] = mat[i][j];
            }
        }

        // Replace the original matrix with the rotated matrix
        mat.Clear();
        mat.AddRange(newMat);
    }

    // Function to display a matrix
    static void DisplayMatrix(List<List<int>> mat)
    {
        int n = mat.Count;      // Number of rows in the matrix
        int m = mat[0].Count;   // Number of columns in the matrix
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                Console.Write(mat[i][j] + " ");
            }
            Console.WriteLine();
        }
        Console.WriteLine();
    }

    static void Main(string[] args)
    {
        // Test Case 1: Define a 3x4 matrix
        List<List<int>> mat = new List<List<int>>
        {
            new List<int> { 1, 2, 3, 4 },
            new List<int> { 5, 6, 7, 8 },
            new List<int> { 9, 10, 11, 12 },
        };

        // Function call to rotate the matrix
        RotateMatrix(mat);

        // Display the rotated matrix
        DisplayMatrix(mat);
    }
}

Javascript

// Function to rotate a
// 90 x 90 matrix by
// 90 degrees clockwise
function rotateMatrix(mat) {
    const n = mat.length;
    const m = mat[0].length;
    const newMat = new Array(m).fill(0).map(() => new Array(n).fill(0));

    for (let i = 0; i < n; i++) {
        for (let j = 0; j < m; j++) {
            newMat[j][n - i - 1] = mat[i][j];
        }
    }

    return newMat;
}

// Function to print the matrix
function displayMatrix(mat) {
    const n = mat.length;
    const m = mat[0].length;
    for (let i = 0; i < n; i++) {
        let row = '';
        for (let j = 0; j < m; j++) {
            row += mat[i][j] + ' ';
        }
        console.log(row);
    }
    console.log('');
}

// Driver code

// Test Case 1
const mat = [
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
];

// Function call
const rotatedMat = rotateMatrix(mat);

// Print rotated matrix
displayMatrix(rotatedMat);

Output

9 5 1 
10 6 2 
11 7 3 
12 8 4 

Time Complexity: O(N*M), as we are using nested loops for traversing the matrix.

Auxiliary Space: O(N*M), as we are using extra space for new matrix.

Another Approach:

Following are the steps of this approach:

• Transposition: The transposed_image matrix is created by swapping the rows and columns of the input image. This is achieved by iterating over the rows and columns of the input image and creates a new matrix where the rows and columns are swapped.
• Reverse Rows: The rotated_image matrix is created by reversing the order of rows in the transposed_image matrix. This step effectively rotates the image by 90 degrees clockwise.

• Finally, the rotated image is printed by iterating over the rows of rotated_image matrix and printing them.

C++

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;

int main()
{
    // Define input image as a 2D vector of pixels
    vector<vector<int> > image = { { 1, 2, 3, 4 },
                                   { 5, 6, 7, 8 },
                                   { 9, 10, 11, 12 } };

    // Transpose image matrix
    vector<vector<int> > transposed_image(
        image[0].size(), vector<int>(image.size()));
    for (int i = 0; i < image.size(); i++) {
        for (int j = 0; j < image[0].size(); j++) {
            transposed_image[j][i] = image[i][j];
        }
    }

    // Reverse the order of rows to rotate the image by 90
    // degrees clockwise
    vector<vector<int> > rotated_image(
        transposed_image.size());
    for (int i = 0; i < transposed_image.size(); i++) {
        rotated_image[i]
            = vector<int>(transposed_image[i].rbegin(),
                          transposed_image[i].rend());
    }

    // Print rotated image
    for (int i = 0; i < rotated_image.size(); i++) {
        cout << '[';
        for (int j = 0; j < rotated_image[0].size(); j++) {
            cout << rotated_image[i][j];
            if (j < rotated_image[0].size() - 1)
                cout << ", ";
        }
        cout << "]" << endl;
    }
    return 0;
}

Java

import java.util.ArrayList;

public class ImageRotation {
    public static void main(String[] args) {
        // Define input image as a 2D ArrayList of pixels
        ArrayList<ArrayList<Integer>> image = new ArrayList<>();
        image.add(new ArrayList<Integer>() {{
            add(1);
            add(2);
            add(3);
            add(4);
        }});
        image.add(new ArrayList<Integer>() {{
            add(5);
            add(6);
            add(7);
            add(8);
        }});
        image.add(new ArrayList<Integer>() {{
            add(9);
            add(10);
            add(11);
            add(12);
        }});

        // Transpose image matrix
        ArrayList<ArrayList<Integer>> transposedImage = new ArrayList<>();
        for (int i = 0; i < image.get(0).size(); i++) {
            ArrayList<Integer> row = new ArrayList<>();
            for (int j = 0; j < image.size(); j++) {
                row.add(image.get(j).get(i));
            }
            transposedImage.add(row);
        }

        // Reverse the order of rows to rotate the image by 90 degrees counterclockwise
        ArrayList<ArrayList<Integer>> rotatedImage = new ArrayList<>();
        for (int i = 0; i < transposedImage.size(); i++) {
            ArrayList<Integer> row = new ArrayList<>();
            for (int j = transposedImage.get(i).size() - 1; j >= 0; j--) {
                row.add(transposedImage.get(i).get(j));
            }
            rotatedImage.add(row);
        }

        // Print rotated image
        for (int i = 0; i < rotatedImage.size(); i++) {
            System.out.print("[");
            for (int j = 0; j < rotatedImage.get(0).size(); j++) {
                System.out.print(rotatedImage.get(i).get(j));
                if (j < rotatedImage.get(0).size() - 1) {
                    System.out.print(", ");
                }
            }
            System.out.println("]");
        }
    }
}

Python3

# define input image as a 2D list of pixels
image = [[1, 2, 3, 4],
         [5, 6, 7, 8],
         [9, 10, 11, 12]]

# transpose image matrix
transposed_image = [[image[j][i] for j in range(len(image))] for i in range(len(image[0]))]

# reverse the order of rows to rotate the image by 90 degrees counterclockwise
rotated_image = [list(reversed(row)) for row in transposed_image]

# print rotated image
for row in rotated_image:
    print(row)

C#

using System;

class Program {
    static void Main(string[] args)
    {
        // Define input image as a 2D array of pixels
        int[, ] image = new int[, ] { { 1, 2, 3, 4 },
                                      { 5, 6, 7, 8 },
                                      { 9, 10, 11, 12 } };

        // Transpose image matrix
        int[, ] transposed_image
            = new int[image.GetLength(1),
                      image.GetLength(0)];
        for (int i = 0; i < image.GetLength(0); i++) {
            for (int j = 0; j < image.GetLength(1); j++) {
                transposed_image[j, i] = image[i, j];
            }
        }

        // Reverse the order of columns to rotate the image
        // by 90 degrees counterclockwise
        int[, ] rotated_image
            = new int[transposed_image.GetLength(0),
                      transposed_image.GetLength(1)];
        for (int i = 0; i < transposed_image.GetLength(0);
             i++) {
            for (int j = 0;
                 j < transposed_image.GetLength(1); j++) {
                rotated_image[i, j] = transposed_image
                    [i,
                     transposed_image.GetLength(1) - 1 - j];
            }
        }

        // Print rotated image
        for (int i = 0; i < rotated_image.GetLength(0);
             i++) {
            Console.Write("[");
            for (int j = 0; j < rotated_image.GetLength(1);
                 j++) {
                Console.Write(rotated_image[i, j] + ", ");
            }
            Console.WriteLine("]");
        }
    }
}

Javascript

// define input image as a 2D array of pixels
const image = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]];

// transpose image matrix
const transposedImage = image[0].map((_, i) => image.map(row => row[i]));

// reverse the order of rows to rotate the image by 90 degrees counterclockwise
const rotatedImage = transposedImage.map(row => row.reverse());

// print rotated image
for (let row of rotatedImage) {
console.log(row);
}

Output

[9, 5, 1]
[10, 6, 2]
[11, 7, 3]
[12, 8, 4]

Time Complexity: O(N*M)
Auxiliary Space: O(N*M)

Refer to the below article for rotating the square matrix by 90 degrees inplace (Without modifying input 2D matrix directly).

Inplace rotate square matrix by 90 degrees