Transportation Problem | Set 1 (Introduction)

Transportation problem is a special kind of Linear Programming Problem (LPP) in which goods are transported from a set of sources to a set of destinations subject to the supply and demand of the sources and destination respectively such that the total cost of transportation is minimized. It is also sometimes called as Hitchcock problem.

Types of Transportation problems:
Balanced: When both supplies and demands are equal then the problem is said to be a balanced transportation problem.

Unbalanced: When the supply and demand are not equal then it is said to be an unbalanced transportation problem. In this type of problem, either a dummy row or a dummy column is added according to the requirement to make it a balanced problem. Then it can be solved similar to the balanced problem.

Methods to Solve:
To find the initial basic feasible solution there are three methods:

1. NorthWest Corner Cell Method.
2. Least Cost Method.
3. Vogel’s Approximation Method (VAM).

Basic structure of transportation problem:

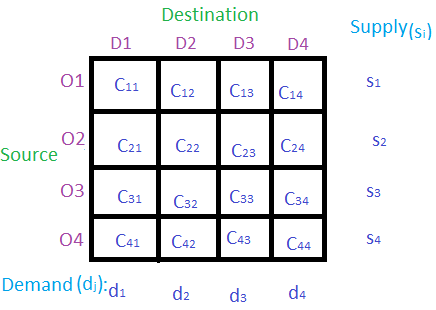
In the above table D1, D2, D3 and D4 are the destinations where the products/goods are to be delivered from different sources S1, S2, S3 and S4. S_i is the supply from the source O_i. d_j is the demand of the destination D_j. C_ij is the cost when the product is delivered from source S_i to destination D_j.