std::cyl_bessel_i in C++17

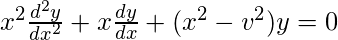
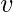
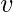
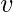
In Mathematics, the differential equation, is of particular importance. The solution of the equation is a function of the parameter . For integral and half-integral values of , the solutions of particular interest and are called as Cylindrical Bessel’s Functions, named after the famous German mathematician, Friedrich Wilhelm Bessel. The reason for the requirement of to be integral or half-integral will be clear in the explanation given below. Since this is a second-order differential equation, there must be two linearly independent solutions, called as the first kind and the second kind. Thus, the differential equation can be solved by hand using the Frobenius Method. 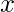Bessel functions of the first kind, for complex arguments , are called Modified Bessel Functions of the first kind and are denoted by . 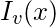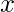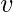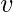The application of the method produces an infinite series containing terms of and , given by, Since the expression contains Gamma Function, which can only be calculated for integral and half-integral values, thus the parameter must be integral or half-integral. C++17 (GCC 7.1) Standard Library cmath gives functions which compute the value of the Cylindrical Bessel’s Function of the first kind (std::cyl_bessel_j) (not discussed here, but is very similar to what we have discussed) and the value of Regular Modified Bessel Functions (std::cyl_bessel_i). Both have appreciable accuracy for small inputs and can be used in various engineering applications. Examples:

Input: x = 2.798465, v = 0 Output: 4.152234090041574 Input: x = 3.04513, v = 0.5 Output: 4.792979684692604

Note: The following source code should only be run on C++17 and above. The running sample of the given code can be checked here. To run for a different input, please visit the link and click “Edit” in the bottom right corner.

// C++17 code for bessel function
#include <bits/stdc++.h>
using namespace std;

// Compute the answer from the formulae for first 10 terms
long double answer(long double x, long double v)
{

    long double ans_by_expansion = 0;
    long double fact = 1;

    for (int k = 0; k < 10; fact = fact * (++k)) {
        ans_by_expansion += pow((x / 2), (2 * k)) / pow(fact, 2);
        cout << "ans_by_expansion till term k = ";
        cout << k << " is " << ans_by_expansion << "\n";
    }

  return ans_by_expansion;
}

// Driver code
int main()
{
    long double x = 2.798465;
    long double v = 0;

    // Compute the Regular Modified Bessel Function
    // for v = 0, x = 2.798465
    long double ans_by_function = cyl_bessel_i(v, x);

    cout << setprecision(15) << fixed;
    cout << "The answer by function for "
         << "Regular_Modified_Bessel_Function" << endl
         << "(" << v << ", " << x << ") = "
         << ans_by_function << "\n";

    // calculate answer by expansion
    long double ans_by_expansion = answer(x, v);

    cout << "Absolute Error in answer by both the methods is = ";
    cout << abs(ans_by_expansion - ans_by_function) << "\n";

    return 0;
}

Output:

The answer by function for Regular_Modified_Bessel_Function
(0.000000000000000, 2.798465000000000) = 4.152234090041574
ans_by_expansion till term k = 0 is 1.000000000000000
ans_by_expansion till term k = 1 is 2.957851589056250
ans_by_expansion till term k = 2 is 3.916147300248771
ans_by_expansion till term k = 3 is 4.124614053687001
ans_by_expansion till term k = 4 is 4.150123238967278
ans_by_expansion till term k = 5 is 4.152120966924739
ans_by_expansion till term k = 6 is 4.152229612892962
ans_by_expansion till term k = 7 is 4.152233953968095
ans_by_expansion till term k = 8 is 4.152234086767796
ans_by_expansion till term k = 9 is 4.152234089977698
Absolute Error in answer by both the methods is = 0.000000000063876