Schröder–Hipparchus number

The Schröder–Hipparchus numbers form an integer sequence that can be used to count the number of plane trees with a given set of leaves, the number of ways of inserting parentheses into a sequence, and the number of ways of dissecting a convex polygon into smaller polygons by inserting diagonals. 

Schröder–Hipparchus number can be define by recurrence relation: 

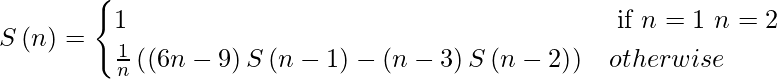
Schröder–Hipparchus number can be used to count several closely related combinatorial objects:  

1. The nth number in the sequence counts the number of different ways of subdividing of a polygon with n + 1 sides into smaller polygons by adding diagonals of the original polygon. Refer this image for details.
   Image source: Wikipedia
2. The nth number counts the number of different plane trees with n leaves and with all internal vertices having two or more children.
3. The nth number counts the number of different ways of inserting parentheses into a sequence of n symbols, with each pair of parentheses surrounding two or more symbols or parenthesized groups, and without any parentheses surrounding the entire sequence.
4. The nth number counts the number of faces of all dimensions of an associahedron Kn + 1 of dimension n ? 1, including the associahedron itself as a face, but not including the empty set. For instance, the two-dimensional associahedron K4 is a pentagon; it has five vertices, five faces, and one whole associahedron, for a total of 11 faces.
5. count the number of double permutations (sequences of the numbers from 1 to n, each number appearing twice, with the first occurrences of each number in sorted order) that avoid the permutation patterns 12312 and 121323.

Examples:

Input : n = 5
Output : 45

Input : n = 6
Output : 197

A simple solution is simply to implement a recursive formula for the numbers.  

C++

// A simple recursive CPP program to find n-th
// Schröder–Hipparchus number
#include <bits/stdc++.h>
using namespace std;
int nthSHN(int n)
{
    if (n == 1 || n == 2)
        return 1;

    return ((6 * n - 9) * nthSHN(n - 1) -
           (n - 3) * nthSHN(n - 2)) / n;
}

// Driven Program
int main()
{
    int n = 6;
    cout << nthSHN(n) << endl;
    return 0;
}

Java

// A simple recursive Java program to
// find n-th Schroder-Hipparchus number
class GFG
{
static int nthSHN(int n)
{
    if (n == 1 || n == 2)
        return 1;

    return ((6 * n - 9) * nthSHN(n - 1) -
        (n - 3) * nthSHN(n - 2)) / n;
}

// Driver code
public static void main (String[] args)
{
    int n = 6;
    System.out.println(nthSHN(n));
}
}

// This code is contributed by Anant Agarwal.

Python3

# A simple recursive Python3 program to
# find n-th Schröder–Hipparchus numberr

def nthSHN(n):
    if (n == 1 or n == 2):
        return 1
    else:
        return ((6 * n - 9) * nthSHN(n - 1) -
               ((n - 3) * nthSHN(n - 2))) / n

# Driven Program
n = 6
print (nthSHN(n))

# This code is contributed by Sachin Bisht

C#

// A simple recursive C# program to
// find n-th Schroder-Hipparchus number
using System;

class GFG
{
    static int nthSHN(int n)
    {
        if (n == 1 || n == 2)
            return 1;

        return ((6 * n - 9) * nthSHN(n - 1) -
                (n - 3) * nthSHN(n - 2)) / n;
    }

    // Driver code
    public static void Main ()
    {
        int n = 6;
        Console.WriteLine(nthSHN(n));
    }
}

// This code is contributed by vt_m.

PHP

<?php
// A simple recursive PHP
// program to find n-th
// Schröder–Hipparchus number

// function returns the n-th
// Schröder–Hipparchus number
function nthSHN( $n)
{
    if ($n == 1 || $n == 2)
        return 1;

    return ((6 * $n - 9) * nthSHN($n - 1) -
           ($n - 3) * nthSHN($n - 2)) / $n;
}

    // Driver Program
    $n = 6;
    echo nthSHN($n);

// This code is contributed by anuj_67.
?>

Javascript

<script>

// Javascript Program to
// find n-th Schroder-Hipparchus number
function nthSHN(n)
{
    if (n == 1 || n == 2)
        return 1;

    return ((6 * n - 9) * nthSHN(n - 1) -
                (n - 3) * nthSHN(n - 2)) / n;
}

// Driver code
let n = 6;

document.write(nthSHN(n));

// This code is contributed by sanjoy_62

</script>

Output: 

197

Time Complexity: O(2^n)

Auxiliary Space: O(n) since the maximum number of function calls is n.

Below is Dynamic Programming solution of finding nth Schröder–Hipparchus number: 

C++

// A memoization based optimized CPP program to
// find n-th Schröder–Hipparchus number
#include <bits/stdc++.h>
#define MAX 500
using namespace std;

int nthSHN(int n, int dp[])
{
    if (n == 1 || n == 2)
        return dp[n] = 1;

    if (dp[n] != -1)
        return dp[n];

    return dp[n] = ((6 * n - 9) * nthSHN(n - 1, dp) -
                   (n - 3) * nthSHN(n - 2, dp)) / n;
}

// Driven Program
int main()
{
    int n = 6;
    int dp[MAX];
    memset(dp, -1, sizeof dp);
    cout << nthSHN(n, dp) << endl;
    return 0;
}

Java

// A memoization based optimized
// Java program to find n-th
// Schroder-Hipparchus number
import java.util.Arrays;

class GFG
{
static final int MAX=500;

static int nthSHN(int n, int dp[])
{
    if (n == 1 || n == 2)
        return dp[n] = 1;

    if (dp[n] != -1)
        return dp[n];

    return dp[n] = ((6 * n - 9) * nthSHN(n - 1, dp) -
                     (n - 3) * nthSHN(n - 2, dp)) / n;
}

// Driver code
public static void main (String[] args)
{
    int n = 6;
    int dp[] = new int[MAX];
    Arrays.fill(dp, -1);
    System.out.println(nthSHN(n, dp));
}
}

// This code is contributed by Anant Agarwal.

Python3

# A memoization based optimized
# Python3 program to find n-th
# Schröder–Hipparchus number

def nthSHN(n, dp):
    if (n == 1 or n == 2):
        dp[n] = 1
        return dp[n]

    if (dp[n] != -1):
        return dp[n]

    dp[n] = ((6 * n - 9) * nthSHN(n - 1, dp) -
             (n - 3) * nthSHN(n - 2, dp)) / n
    return dp[n]

# Driven Program
n = 6;
dp = [-1 for i in range(500)]
print (nthSHN(n, dp))

# This code is contributed by Sachin Bisht

C#

// A memoization based optimized
// C# program to find n-th
// Schroder-Hipparchus number
using System;

class GFG
{
static int MAX = 500;

static int nthSHN(int n, int[] dp)
{
    if (n == 1 || n == 2)
        return dp[n] = 1;

    if (dp[n] != -1)
        return dp[n];

    return dp[n] = ((6 * n - 9) *
                     nthSHN(n - 1, dp) -
                    (n - 3) *
                     nthSHN(n - 2, dp)) / n;
}

// Driver code
public static void Main ()
{
    int n = 6;
    int[] dp = new int[MAX];
    for(int i = 0; i < dp.Length; i++)
    dp[i] = -1;
    Console.Write(nthSHN(n, dp));
}
}

// This code is contributed by mits.

PHP

<?php
// A memoization based optimized
// PHP program to find n-th
// Schröder–Hipparchus number
$MAX = 500;

function nthSHN($n, $dp)
{
    if ($n == 1 || $n == 2)
        return $dp[$n] = 1;

    if ($dp[$n] != -1)
        return $dp[$n];

    return $dp[$n] = ((6 * $n - 9) *
                       nthSHN($n - 1, $dp) -
                      ($n - 3) *
                       nthSHN($n - 2, $dp)) / $n;
}

// Driver Code
$n = 6;

$dp=array_fill(0, $MAX, true);
echo nthSHN($n, $dp), "\n";

// This code is contributed by ajit
?>

Javascript

<script>
    // A memoization based optimized
    // Javascript program to find n-th
    // Schroder-Hipparchus number

    let MAX = 500;

    function nthSHN(n, dp)
    {
        if (n == 1 || n == 2)
            return dp[n] = 1;

        if (dp[n] != -1)
            return dp[n];

        return dp[n] = ((6 * n - 9) * nthSHN(n - 1, dp) - (n - 3) * nthSHN(n - 2, dp)) / n;
    }

    let n = 6;
    let dp = new Array(MAX);
    for(let i = 0; i < dp.length; i++)
        dp[i] = -1;
    document.write(nthSHN(n, dp));

</script>

Output:

197

Time Complexity: O(n)

Auxiliary Space: O(n)

Source: 
https://en.wikipedia.org/wiki/Schr%C3%B6der%E2%80%93Hipparchus_number