Relationship between AM, GM and HM
Last Updated :
29 Sep, 2023
Several measures of central tendency, or averages, are available, each of which is typical in some unique way and has particular characteristics. The commonly used averages are Arithmetic Mean (AM), Geometric Mean (GM), and Harmonic Mean (HM). Further, there exists a very important relationship between AM, GM, and HM.
Arithmetic Mean (AM)
Arithmetic Mean is calculated as the simple average of all the observations. The value of this average is obtained by dividing the sum of the observations by their number. The arithmetic mean provides a measure of central tendency and is commonly used to find the average of a set of data points. This is simply referred to as mean and is represented by 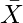 .
.

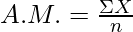
Geometric Mean (GM)
Geometric Mean is calculated as the nth root of the product of n values. The geometric mean is useful for calculating the average rates of change, such as compound interest rates or growth rates of investments. The geometric mean tends to reduce the impact of extreme values and is often used in financial and scientific contexts.
![Rendered by QuickLaTeX.com G.M.=\sqrt[n]{X_1\times{X_2}\times{X_3}\times{X_4}\times.......X_n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56457fbcb3210d4e26bb3b8fad821c99_l3.png)
Harmonic Mean (HM)
Harmonic Mean is defined as the reciprocal of the arithmetic mean of reciprocals. It is particularly used in situations where someone needs to find an average that reflects the ‘rate of work’ or ‘rate of speed.’
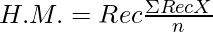
Relationship between AM, GM and HM
1. For any set of unequal positive numbers, the relationship between AM, GM, and HM is expressed as: AM > GM > HM.
2. If the values in the set data are equal, then the three averages would also be equal.
In case of set of two numbers, the relationship between AM, GM, and HM is expressed as:
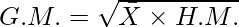
They depict this relationship; let’s take two numbers, a and b:
We know that,
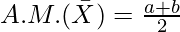
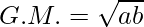
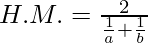
Multiplying AM and HM, we get,
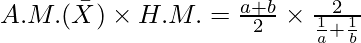
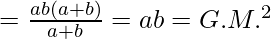
Thus, we have 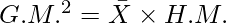 or
or 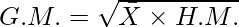
Example 1:
Find the harmonic mean of two numbers a and b, if the arithmetic mean is 25 and the geometric mean is 10 provided that a>b>0.
Solution:
Given, A.M. = 25 and G.M. = 10
The relationship between AM, GM, and HM is, 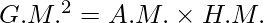
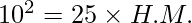
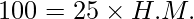
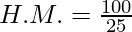
H.M. = 4
Example 2:
Show that 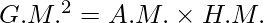 , using numbers 16 and 4.
, using numbers 16 and 4.
Solution:
Here, 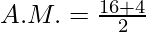
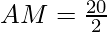
AM = 10
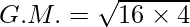
G.M. = 8
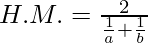
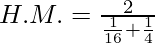
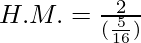
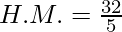
H.M. = 6.4
Verifying relationship, 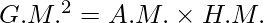
82 = 10 x 6.4
Hence, 64 = 64.
Share your thoughts in the comments
Please Login to comment...