Rearrange an array in maximum minimum form using Two Pointer Technique
Last Updated :
14 Dec, 2022
Given a sorted array of positive integers, rearrange the array alternately i.e first element should be a maximum value, at second position minimum value, at third position second max, at fourth position second min, and so on.
Examples:
Input: arr[] = {1, 2, 3, 4, 5, 6, 7}
Output: arr[] = {7, 1, 6, 2, 5, 3, 4}
Input: arr[] = {1, 2, 3, 4, 5, 6}
Output: arr[] = {6, 1, 5, 2, 4, 3}
Rearrange an array in maximum minimum form using Two Pointers:
The idea is to use an auxiliary array. We maintain two pointers one to the leftmost or smallest element and the other to the rightmost or largest element. We move both pointers toward each other and alternatively copy elements at these pointers to an auxiliary array. Finally, we copy the auxiliary array back to the original array.
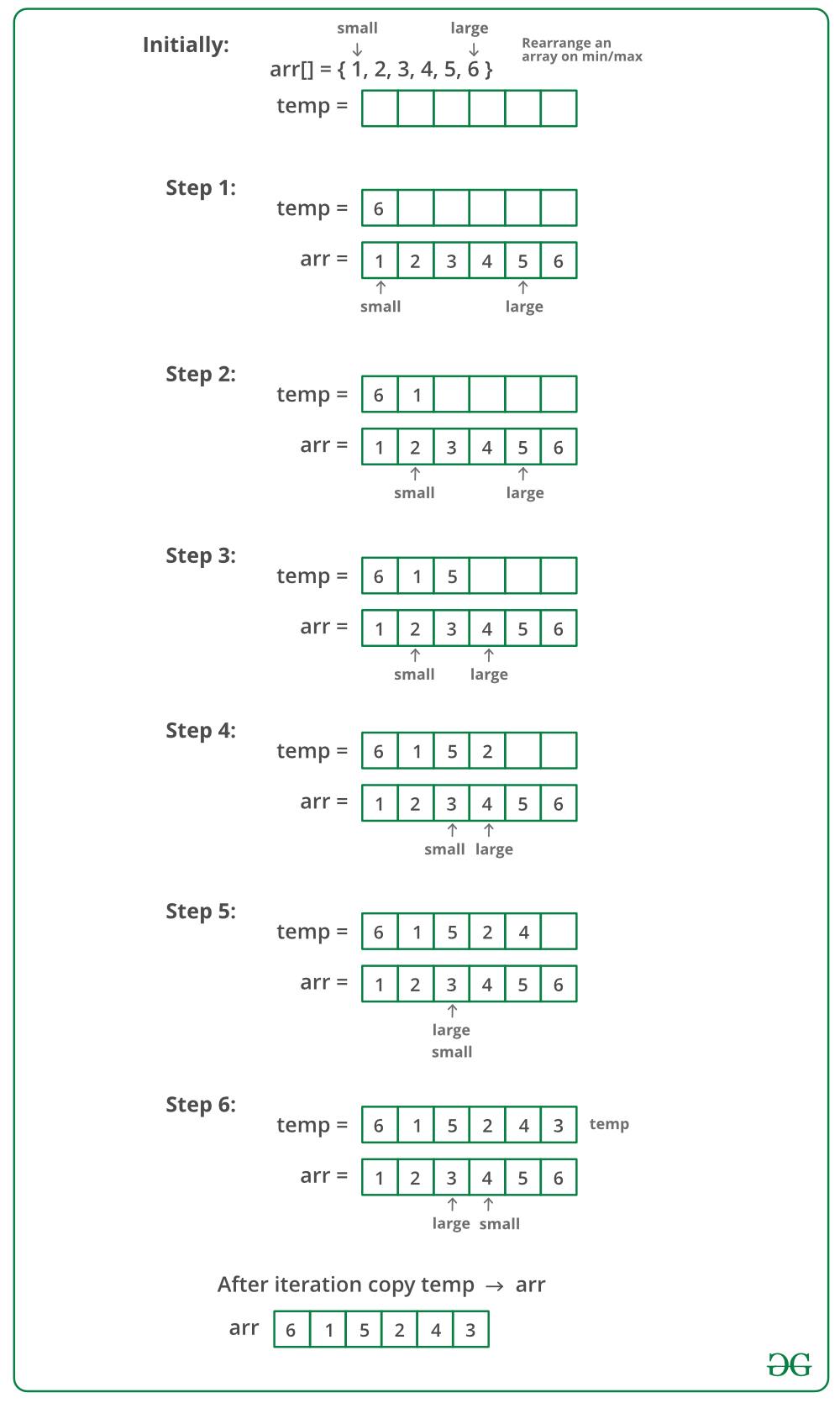
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void rearrange(int arr[], int n)
{
int temp[n];
int small = 0, large = n - 1;
int flag = true;
for (int i = 0; i < n; i++) {
if (flag)
temp[i] = arr[large--];
else
temp[i] = arr[small++];
flag = !flag;
}
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
int main()
{
int arr[] = { 1, 2, 3, 4, 5, 6 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << "Original Array\n";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
rearrange(arr, n);
cout << "\nModified Array\n";
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
return 0;
}
|
Java
import java.util.Arrays;
public class GFG
{
static void rearrange(int[] arr, int n)
{
int temp[] = arr.clone();
int small = 0, large = n - 1;
boolean flag = true;
for (int i = 0; i < n; i++) {
if (flag)
arr[i] = temp[large--];
else
arr[i] = temp[small++];
flag = !flag;
}
}
public static void main(String[] args)
{
int arr[] = new int[] { 1, 2, 3, 4, 5, 6 };
System.out.println("Original Array ");
System.out.println(Arrays.toString(arr));
rearrange(arr, arr.length);
System.out.println("Modified Array ");
System.out.println(Arrays.toString(arr));
}
}
|
Python3
def rearrange(arr, n):
temp = n*[None]
small, large = 0, n-1
flag = True
for i in range(n):
if flag is True:
temp[i] = arr[large]
large -= 1
else:
temp[i] = arr[small]
small += 1
flag = bool(1-flag)
for i in range(n):
arr[i] = temp[i]
return arr
arr = [1, 2, 3, 4, 5, 6]
n = len(arr)
print("Original Array")
print(arr)
print("Modified Array")
print(rearrange(arr, n))
|
C#
using System;
class GFG {
static void rearrange(int[] arr, int n)
{
int[] temp = new int[n];
int small = 0, large = n - 1;
bool flag = true;
for (int i = 0; i < n; i++) {
if (flag)
temp[i] = arr[large--];
else
temp[i] = arr[small++];
flag = !flag;
}
for (int i = 0; i < n; i++)
arr[i] = temp[i];
}
static void Main()
{
int[] arr = { 1, 2, 3, 4, 5, 6 };
Console.WriteLine("Original Array");
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
rearrange(arr, arr.Length);
Console.WriteLine("\nModified Array");
for (int i = 0; i < arr.Length; i++)
Console.Write(arr[i] + " ");
}
}
|
PHP
<?php
function rearrange(&$arr, $n)
{
$temp = array();
$small = 0;
$large = $n - 1;
$flag = true;
for ($i = 0; $i < $n; $i++)
{
if ($flag)
$temp[$i] = $arr[$large--];
else
$temp[$i] = $arr[$small++];
$flag = !$flag;
}
for ($i = 0; $i < $n; $i++)
$arr[$i] = $temp[$i];
}
$arr = array(1, 2, 3, 4, 5, 6);
$n = count($arr);
echo "Original Arrayn\n";
for ($i = 0; $i < $n; $i++)
echo $arr[$i] . " ";
rearrange($arr, $n);
echo "\nModified Arrayn\n";
for ($i = 0; $i < $n; $i++)
echo $arr[$i] . " ";
?>
|
Javascript
<script>
function rearrange(arr, n)
{
let temp = new Array(n);
let small = 0, large = n - 1;
let flag = true;
for (let i = 0; i < n; i++) {
if (flag)
temp[i] = arr[large--];
else
temp[i] = arr[small++];
flag = !flag;
}
for (let i = 0; i < n; i++)
arr[i] = temp[i];
}
let arr = [ 1, 2, 3, 4, 5, 6 ];
let n = arr.length;
document.write("Original Array<br>");
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
rearrange(arr, n);
document.write("<br>Modified Array<br>");
for (let i = 0; i < n; i++)
document.write(arr[i] + " ");
</script>
|
Output
Original Array
1 2 3 4 5 6
Modified Array
6 1 5 2 4 3
Time Complexity: O(N), Iterating over the array of size N 2 times.
Auxiliary Space: O(N), since N extra space has been taken.
Exercise: How to solve this problem if extra space is not allowed?
Rearrange an array in maximum minimum form | Set 2 (O(1) extra space)
Share your thoughts in the comments
Please Login to comment...