Orbit counting theorem or Burnside’s Lemma
Last Updated :
16 Sep, 2022
Burnside’s Lemma is also sometimes known as orbit counting theorem. It is one of the results of group theory. It is used to count distinct objects with respect to symmetry. It basically gives us the formula to count the total number of combinations, where two objects that are symmetrical to each other with respect to rotation or reflection are counted as a single representative.
Therefore, Burnside Lemma’s states that total number of distinct object is: 
where:
- c(k) is the number of combination that remains unchanged when Kth rotation is applied, and
- N is the total number of ways to change the position of N elements.
For Example:
Let us consider we have a necklace of N stones and we can color it with M colors. If two necklaces are similar after rotation then the two necklaces are considered to be similar and counted as one different combination. Now Let’s suppose we have N = 4 stones with M = 3 colors, then
Since we have N stones, therefore, we have N possible variations of each necklace by rotation:
Observations: There are N ways to change the position of the necklace as we can rotate it by 0 to N – 1 time.
- There are
 ways to color a necklace. If the number of rotations is 0, then all
ways to color a necklace. If the number of rotations is 0, then all  ways remain different.
ways remain different. - If the number of rotation is 1, then there are only M necklaces which will be different out of all
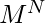 ways.
ways. - Generally, if the number of rotations is K,
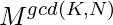 necklaces will remain the same out of all
necklaces will remain the same out of all 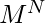 ways.
ways.
Therefore, for a total number of distinct necklaces of N stones after coloring with M colors is the summation of all the distinct necklaces at each rotation. It is given by:
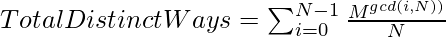
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void countDistinctWays(int N, int M)
{
int ans = 0;
for (int i = 0; i < N; i++) {
int K = __gcd(i, N);
ans += pow(M, K);
}
ans /= N;
cout << ans << endl;
}
int main()
{
int N = 4, M = 3;
countDistinctWays(N, M);
return 0;
}
|
Java
class GFG{
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static void countDistinctWays(int N, int M)
{
int ans = 0;
for(int i = 0; i < N; i++)
{
int K = gcd(i, N);
ans += Math.pow(M, K);
}
ans /= N;
System.out.print(ans);
}
public static void main(String []args)
{
int N = 4, M = 3;
countDistinctWays(N, M);
}
}
|
Python3
from math import gcd
def countDistinctWays(N, M):
ans = 0;
for i in range(N):
K = gcd(i, N);
ans += pow(M, K);
ans //= N;
print(ans);
N = 4
M = 3;
countDistinctWays(N, M);
|
C#
using System;
class GFG
{
static int gcd(int a, int b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
static void countDistinctWays(int N, int M)
{
int ans = 0;
for(int i = 0; i < N; i++)
{
int K = gcd(i, N);
ans += (int)Math.Pow(M, K);
}
ans /= N;
Console.Write(ans);
}
public static void Main(string []args)
{
int N = 4, M = 3;
countDistinctWays(N, M);
}
}
|
Javascript
<script>
function gcd(a, b)
{
if (a == 0)
return b;
return gcd(b % a, a);
}
function countDistinctWays(N, M)
{
let ans = 0;
for(let i = 0; i < N; i++)
{
let K = gcd(i, N);
ans += Math.pow(M, K);
}
ans /= N;
document.write(ans);
}
let N = 4, M = 3;
countDistinctWays(N, M);
</script>
|
Share your thoughts in the comments
Please Login to comment...