Number of Symmetric Relations on a Set
Last Updated :
19 May, 2022
Given a number n, find out the number of Symmetric Relations on a set of first n natural numbers {1, 2, ..n}.
Examples:
Input : n = 2
Output : 8
Given set is {1, 2}. Below are all symmetric relation.
{}
{(1, 1)},
{(2, 2)},
{(1, 1), (2, 2)},
{(1, 2), (2, 1)}
{(1, 1), (1, 2), (2, 1)},
{(2, 2), (1, 2), (2, 1)},
{(1, 1), (2, 2), (2, 1), (1, 2)}
Input : n = 3
Output : 64
A Relation ‘R’ on Set A is said be Symmetric if xRy then yRx for every x, y ? A
or if (x, y) ? R, then (y, x) ? R for every x, y?A
Total number of symmetric relations is 2n(n+1)/2.
How does this formula work?
A relation R is symmetric if the value of every cell (i, j) is same as that cell (j, i). The diagonals can have any value.
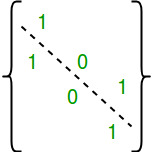
There are n diagonal values, total possible combination of diagonal values = 2n
There are n2 – n non-diagonal values. We can only choose different value for half of them, because when we choose a value for cell (i, j), cell (j, i) gets same value.
So combination of non-diagonal values = 2(n2 – n)/2
Overall combination = 2n * 2(n2 – n)/2 = 2n(n+1)/2
C++
#include <bits/stdc++.h>
unsigned int countSymmetric(unsigned int n)
{
if (n == 0)
return 1;
return 1 << ((n * (n + 1))/2);
}
int main()
{
unsigned int n = 3;
printf("%u", countSymmetric(n));
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int countSymmetric(int n)
{
if (n == 0)
return 1;
return 1 << ((n * (n + 1)) / 2);
}
public static void main (String[] args)
{
int n = 3;
System.out.println(countSymmetric(n));
}
}
|
Python3
def countSymmetric(n) :
if (n == 0) :
return 1
return (1 << ((n * (n + 1))//2))
n = 3
print(countSymmetric(n))
|
C#
using System;
class GFG {
static int countSymmetric(int n)
{
if (n == 0)
return 1;
return 1 << ((n * (n + 1)) / 2);
}
public static void Main ()
{
int n = 3;
Console.WriteLine(countSymmetric(n));
}
}
|
PHP
<?php
function countSymmetric($n)
{
if ($n == 0)
return 1;
return 1 << (($n * ($n + 1))/2);
}
$n = 3;
echo(countSymmetric($n));
?>
|
Javascript
<script>
function countSymmetric(n)
{
if (n == 0)
return 1;
return 1 << ((n * (n + 1)) / 2);
}
let n = 3;
document.write(countSymmetric(n));
</script>
|
Share your thoughts in the comments
Please Login to comment...