Multivariate Optimization – KKT Conditions
Last Updated :
10 Nov, 2021
What’s a multivariate optimization problem?
In a multivariate optimization problem, there are multiple variables that act as decision variables in the optimization problem.
z = f(x1, x2, x3…..xn)
So, when you look at these types of problems a general function z could be some non-linear function of decision variables x1, x2, x3 to xn. So, there are n variables that one could manipulate or choose to optimize this function z. Notice that one could explain univariate optimization using pictures in two dimensions that is because in the x-direction we had the decision variable value and in the y-direction, we had the value of the function. However, if it is multivariate optimization then we have to use pictures in three dimensions and if the decision variables are more than 2 then it is difficult to visualize.
Why we are interested in KKT Conditions?
Multivariate optimization with inequality constraint: In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities. Among them <, >, ≤, ≥ are the popular notation to represent different kinds of inequalities. So if there is given an objective function with more than one decision variable and having an inequality constraint then this is known as so.
Example:
min 2x12 + 4x22
st
3x1 + 2x2 ≤ 12
Here x1 and x2 are two decision variable with inequality constraint 3x1 + 2x2 ≤ 12
So in the case of multivariate optimization with inequality constraints, the necessary conditions for x̄* to be the minimizer is it must be satisfied KKT Conditions. So we are interested in KKT conditions.
KKT Conditions:
KKT stands for Karush–Kuhn–Tucker. In mathematical optimization, the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests (sometimes called first-order necessary conditions) for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied.
So generally multivariate optimization problems contain both equality and inequality constraints.
z = min f(x̄)
st
hi (x̄) = 0, i = 1, 2, …m
gj (x̄) ≤ 0, j = 1, 2, …l
Here we have ‘m’ equality constraint and ‘l’ inequality constraint.
Here are the conditions for multivariate optimization problems with both equality and inequality constraints to be at it is optimum value.
![Rendered by QuickLaTeX.com \nabla f(x^*) + \Sigma _i_=_1^l [\nabla h_i(x^*)] \lambda _i^* + \Sigma _j_=_1^m [\nabla g_j(x^*)] \mu _j^* = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a65b821745322ab3520c83ddba078b0b_l3.png) where,
where,
 = Objective function
= Objective function
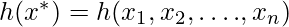 = Equality constraint
= Equality constraint
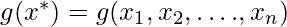 = Inequality constraint
= Inequality constraint
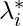 = Scalar multiple for equality constraint
= Scalar multiple for equality constraint
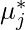 = Scalar multiple for inequality constraint
= Scalar multiple for inequality constraint
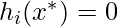 , for i = 1, ...l
, for i = 1, ...l
- This condition ensures that the optimum satisfies equality constraints.
- Condition 3:
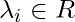 , for i = 1, ..., l
, for i = 1, ..., l
- The lambda must be some real number so as many real numbers as there are in equality constraints.
- Condition 4:
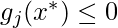 , j = 1, ..., m
, j = 1, ..., m
- Much like in condition 2 that the optimum satisfies equality constraints, we need to have the inequality constraint also to be satisfied by the optimum point. So this ensures that the optimum point is in the feasible region.
- Condition 5:

- Now, this is the real difference between the equality constraint condition and the inequality constrained situation shows up. And this condition is known as complementary slackness condition. So, what this says is if you take a product of the inequality constraint and the corresponding
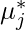 then that has to be 0. Basically what it means is either
then that has to be 0. Basically what it means is either 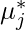 is 0 in which case
is 0 in which case  is free to be any value such that this condition is satisfied or
is free to be any value such that this condition is satisfied or  is 0 in which case we have to compute
is 0 in which case we have to compute 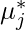 and the
and the 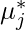 that we compute has to be such that it is a positive number or it is greater than equal to 0.
that we compute has to be such that it is a positive number or it is greater than equal to 0.
- Condition 6:
 , j = 1, .., m
, j = 1, .., m
- In the condition 5 we have seen that either
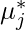 is 0 in which case
is 0 in which case  is free to be any value such that this condition is satisfied or
is free to be any value such that this condition is satisfied or  is 0 in which case we have to compute
is 0 in which case we have to compute 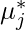 and the
and the 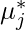 that we compute has to be such that it is a positive number or it is greater than equal to 0. So, this condition is there to ensure that whatever optimum point that you have, there is no possibility of any more improvement from the optimum point. So that is the reason why this condition is there.
that we compute has to be such that it is a positive number or it is greater than equal to 0. So, this condition is there to ensure that whatever optimum point that you have, there is no possibility of any more improvement from the optimum point. So that is the reason why this condition is there.
Share your thoughts in the comments
Please Login to comment...