Minimum difference between the highest and the smallest value of mines distributed
Last Updated :
30 Mar, 2023
Given n companies and m oil mines having values, the task is to distribute the mines among n companies in a fair manner. That is the difference between the company getting the highest sum of values of mines and the one getting the lowest should be minimum. Compute the minimum difference. Note that oil mines distributed to each company should be adjacent to each other. Also, 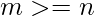
Examples:
Input: n = 2, m = 4 values of mines = [6, 10, 13, 2]
Output: 1 –> mines distributed as {(6, 10), (13, 2)}, hence output is (6+10) – (13+2) = 1
Input: n = 3, m = 4 values of mines = [6, 10, 13, 2]
Output: 9 –> mines distributed as {(6), (10), (13, 2)}, hence output is (13+2) – (6) = 9
Source: Samsung RnD 3 hrs coding round question
Approach:
- Construct an array such that value at each index contains the sum of current and all previous values in the array.
- Include the last value in the array in our solution array.
- Recursively construct all the possible solution arrays by selecting n-1 values from the given m-1 values starting from the second last index (As the last value in the array has already been included in our solution array).
- Subtract the value at next index from the value at current index in the solution array for values at each index except the last value. Calculate the difference between the highest and the lowest value for all the solution arrays and return the minimum.
Let’s take an example to understand the above approach step by step: Initially, the input is provided as below:

After Step 1, our array looks like the array given below :

After Step 2, the solution array looks like the array given below:

After Step 3, we get the following possible solution arrays:

After Step 4, our solution arrays look like the arrays given below. Then we compute the difference between the maximum and minimum value in the array for all the arrays and return the one which is minimum (in this case 9).

Below is the implementation of the above approach:
C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int Func(vector<int> solArr, vector<int> arr, int index, int n)
{
if (n == 0)
{
for (int i = 0; i < solArr.size() - 1; i++)
{
solArr[i] = solArr[i] - solArr[i + 1];
}
return *max_element(solArr.begin(), solArr.end()) - *min_element(solArr.begin(), solArr.end());
}
else
{
if (index >= n)
{
solArr.push_back(arr[index]);
int diff1 = Func(solArr, arr, index - 1, n - 1);
solArr.pop_back();
int diff2 = Func(solArr, arr, index - 1, n);
return min(diff1, diff2);
}
else
{
solArr.push_back(arr[index]);
return Func(solArr, arr, index - 1, n - 1);
}
}
}
int main()
{
int n = 3;
vector<int> arr = { 6, 10, 13, 2 };
for (int i = 1; i < arr.size(); i++)
{
arr[i] += arr[i - 1];
}
vector<int> solArr = { arr[arr.size() - 1] };
cout << Func(solArr, arr, arr.size() - 2, n - 1) << endl;
return 0;
}
|
Java
import java.util.*;
public class Main {
static int func(List<Integer> solArr, int[] arr,
int index, int n)
{
if (n == 0)
{
for (int i = 0; i < solArr.size() - 1; i++) {
solArr.set(i, solArr.get(i) - solArr.get(i + 1));
}
return Collections.max(solArr) - Collections.min(solArr);
}
else
{
if (index >= n)
{
return Math.min(
func(new ArrayList<Integer>(solArr) {{add(arr[index]);}}, arr, index - 1, n - 1),
func(new ArrayList<Integer>(solArr), arr, index - 1, n)
);
}
else
{
return func(new ArrayList<Integer>(solArr) {{add(arr[index]);}}, arr, index - 1, n - 1);
}
}
}
public static void main(String[] args) {
int n = 3;
int[] arr = {6, 10, 13, 2};
for (int i = 1; i < arr.length; i++) {
arr[i] += arr[i - 1];
}
List<Integer> solArr = new ArrayList<Integer>() {{ add(arr[arr.length - 1]); }};
System.out.println(func(new ArrayList<Integer>(solArr), arr, arr.length - 2, n - 1));
}
}
|
Python3
def func(solArr, arr, index, n):
if n == 0:
for i in range(len(solArr)-1):
solArr[i] = solArr[i] - solArr[i + 1]
return max(solArr) - min(solArr)
else:
if index >= n:
return min(func(solArr[:] + [arr[index]], arr, index-1, n-1),
func(solArr[:], arr, index-1, n))
else:
return func(solArr[:] + [arr[index]], arr, index-1, n-1)
n = 3
arr = [6, 10, 13, 2]
for i in range(1, len(arr)):
arr[i] += arr[i-1]
solArr = [arr[-1]]
print(func(solArr[:], arr, len(arr)-2, n-1))
|
C#
using System;
using System.Linq;
class Program
{
static int Func(int[] solArr, int[] arr, int index, int n)
{
if (n == 0)
{
for (int i = 0; i < solArr.Length - 1; i++)
{
solArr[i] = solArr[i] - solArr[i + 1];
}
return solArr.Max() - solArr.Min();
}
else
{
if (index >= n)
{
return Math.Min(
Func(solArr.Concat(new[] { arr[index] }).ToArray(), arr, index - 1, n - 1),
Func(solArr.ToArray(), arr, index - 1, n)
);
}
else
{
return Func(solArr.Concat(new[] { arr[index] }).ToArray(), arr, index - 1, n - 1);
}
}
}
static void Main(string[] args)
{
int n = 3;
int[] arr = { 6, 10, 13, 2 };
for (int i = 1; i < arr.Length; i++)
{
arr[i] += arr[i - 1];
}
int[] solArr = { arr[arr.Length - 1] };
Console.WriteLine(Func(solArr.ToArray(), arr, arr.Length - 2, n - 1));
}
}
|
Javascript
function func(solArr, arr, index, n)
{
if (n == 0) {
for (let i = 0; i < solArr.length - 1; i++) {
solArr[i] = solArr[i] - solArr[i + 1];
}
return Math.max(...solArr) - Math.min(...solArr);
} else {
if (index >= n) {
return Math.min(
func(solArr.concat(arr[index]), arr, index - 1, n - 1),
func(solArr.slice(), arr, index - 1, n)
);
} else {
return func(solArr.concat(arr[index]), arr, index - 1, n - 1);
}
}
}
const n = 3;
const arr = [6, 10, 13, 2];
for (let i = 1; i < arr.length; i++) {
arr[i] += arr[i - 1];
}
const solArr = [arr[arr.length - 1]];
console.log(func(solArr.slice(), arr, arr.length - 2, n - 1));
|
- Time Complexity:
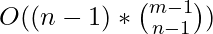
- Space Complexity:
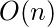
Share your thoughts in the comments
Please Login to comment...