Maximum score after flipping a Binary Matrix atmost K times
Last Updated :
19 Jul, 2022
Given a two dimensional matrix A of zero’s and one’s and an integer K.
In each move, you can choose any row or column and toggle every value in that row or column. That is, change all 0s to 1s, or all 1s to 0s. After making atmost K of moves, every row of this matrix represents a binary number.
The task is to return the maximum possible value of the sum of these numbers.
Examples:
Input : A[][] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
K = 2
Output : 36
Input : A[][] = { { 0, 1 },
{ 1, 0 },
{ 1, 1 } };
K = 1
Output : 7
Notice that a 1 in the i-th column from the right, contributes 2i to the score.
Also knowing the fact that, 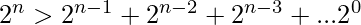 , maximizing the left-most digit is more important than any other digit. Thus, any rows should be toggled such that the left most column should be either all 0 or all 1 (so that after toggling the left-most column [if necessary], the left column is all 1).
, maximizing the left-most digit is more important than any other digit. Thus, any rows should be toggled such that the left most column should be either all 0 or all 1 (so that after toggling the left-most column [if necessary], the left column is all 1).
Now for rows with first element as 0, make a map with value of row as key and index of that row as element. Now we toggle rows with least value so that after updating it contributes maximum to our total score.
Now, for other subsequent columns we count total zeros and ones.
- If ( zeros > ones and K > 0 ) we toggle the column and update our answer to ans = ans + zero * pow( 2, columns – j – 1), for all
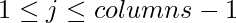 and decrements K by one.
and decrements K by one. - Otherwise we update answer to ans = ans + one * pow( 2, columns – j – 1), for all
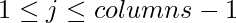 .
.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int n = 3;
const int m = 4;
int maxMatrixScore(int A[n][m], int K)
{
map<int, int> update;
for (int i = 0; i < n; ++i) {
if (A[i][0] == 0) {
int ans = 0;
for (int j = 1; j < m; ++j)
ans = ans + A[i][j] * pow(2, m - j - 1);
update[ans] = i;
}
}
map<int, int>::iterator it = update.begin();
while (K > 0 && it != update.end()) {
int idx = it->second;
for (int j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
it++;
K--;
}
int ans = 0;
for (int j = 0; j < m; ++j) {
int zero = 0, one = 0;
for (int i = 0; i < n; ++i) {
A[i][j] == 0 ? zero++ : one++;
}
if (K > 0 && zero > one) {
ans += zero * pow(2, m - j - 1);
K--;
}
else
ans += one * pow(2, m - j - 1);
}
return ans;
}
int main()
{
int A[n][m] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
cout << maxMatrixScore(A, K);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int n = 3;
static int m = 4;
static int maxMatrixScore(int A[][], int K)
{
HashMap<Integer,Integer> update =
new HashMap<Integer,Integer>();
for (int i = 0; i < n; ++i)
{
if (A[i][0] == 0)
{
int ans = 0;
for (int j = 1; j < m; ++j)
ans = (int) (ans + A[i][j] *
Math.pow(2, m - j - 1));
update.put(ans, i);
}
}
for (Map.Entry<Integer,Integer> it : update.entrySet())
if (K > 0 )
{
int idx = it.getValue();
for (int j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
K--;
}
int ans = 0;
for (int j = 0; j < m; ++j)
{
int zero = 0, one = 0;
for (int i = 0; i < n; ++i)
{
if(A[i][j] == 0)
zero++;
else
one++;
}
if (K > 0 && zero > one)
{
ans += zero * Math.pow(2, m - j - 1);
K--;
}
else
ans += one * Math.pow(2, m - j - 1);
}
return ans;
}
public static void main(String[] args)
{
int A[][] = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
System.out.print(maxMatrixScore(A, K));
}
}
|
Python3
n = 3
m = 4
def maxMatrixScore(A, K):
update = {}
for i in range(0, n):
if A[i][0] == 0:
ans = 0
for j in range(1, m):
ans = ans + A[i][j] * 2 ** (m - j - 1)
update[ans] = i
for idx in update.values():
for j in range(0, m):
A[idx][j] = (A[idx][j] + 1) % 2
K -= 1
if K <= 0:
break
ans = 0
for j in range(0, m):
zero, one = 0, 0
for i in range(0, n):
if A[i][j] == 0: zero += 1
else: one += 1
if K > 0 and zero > one:
ans += zero * 2 ** (m - j - 1)
K -= 1
else:
ans += one * 2 ** (m - j - 1)
return ans
if __name__ == "__main__":
A = [[0, 0, 1, 1],
[1, 0, 1, 0],
[1, 1, 0, 0]]
K = 2
print(maxMatrixScore(A, K))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int n = 3;
static int m = 4;
static int maxMatrixScore(int [,]A, int K)
{
Dictionary<int,int> update =
new Dictionary<int,int>();
int ans=0;
for (int i = 0; i < n; ++i)
{
if (A[i, 0] == 0)
{
ans = 0;
for (int j = 1; j < m; ++j)
ans = (int) (ans + A[i, j] *
Math.Pow(2, m - j - 1));
update.Add((int)ans, i);
}
}
foreach(KeyValuePair<int, int> it in update)
if (K > 0 )
{
int idx = it.Value;
for (int j = 0; j < m; ++j)
A[idx, j] = (A[idx, j] + 1) % 2;
K--;
}
ans = 0;
for (int j = 0; j < m; ++j)
{
int zero = 0, one = 0;
for (int i = 0; i < n; ++i)
{
if(A[i, j] == 0)
zero++;
else
one++;
}
if (K > 0 && zero > one)
{
ans += zero * (int)Math.Pow(2, m - j - 1);
K--;
}
else
ans += one * (int)Math.Pow(2, m - j - 1);
}
return ans;
}
public static void Main(String[] args)
{
int [,]A = { { 0, 0, 1, 1 },
{ 1, 0, 1, 0 },
{ 1, 1, 0, 0 } };
int K = 2;
Console.Write(maxMatrixScore(A, K));
}
}
|
Javascript
<script>
var n = 3;
var m = 4;
function maxMatrixScore(A, K)
{
var update = new Map();
for (var i = 0; i < n; ++i) {
if (A[i][0] == 0) {
var ans = 0;
for (var j = 1; j < m; ++j)
ans = ans + A[i][j] * Math.pow(2, m - j - 1);
update.set(ans, i);
}
}
update.forEach((value, key) => {
if(K>0)
{
var idx = value;
for (var j = 0; j < m; ++j)
A[idx][j] = (A[idx][j] + 1) % 2;
K--;
}
});
var ans = 0;
for (var j = 0; j < m; ++j) {
var zero = 0, one = 0;
for (var i = 0; i < n; ++i) {
A[i][j] == 0 ? zero++ : one++;
}
if (K > 0 && zero > one) {
ans += zero * Math.pow(2, m - j - 1);
K--;
}
else
ans += one * Math.pow(2, m - j - 1);
}
return ans;
}
var A = [ [ 0, 0, 1, 1 ],
[ 1, 0, 1, 0 ],
[ 1, 1, 0, 0 ] ];
var K = 2;
document.write( maxMatrixScore(A, K));
</script>
|
Time Complexity: O(N*M)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...