Long Division Method to find Square root with Examples
Last Updated :
26 Nov, 2021
Given an integer X which is a perfect square, the task is to find the square root of it by using the long division method.
Examples:
Input: N = 484
Output: 22
222 = 484
Input: N = 144
Output: 12
122 = 144
Approach:
Long division is a very common method to find the square root of a number. The following is the stepwise solution for this method:
1. Divide the digits of the number into pairs of segments starting with the digit in the units place. Let’s identify each pair and the remaining final digit(in case there is an odd count of digits in the number) as a segment.
For example:
1225 is divided as (12 25)

2. After dividing the digits into segments, start from the leftmost segment. The largest number whose square is equal to or just less than the first segment is taken as the divisor and also as the quotient (so that the product is the square).
For example:
9 is the closest perfect square to 12, the first segment 12
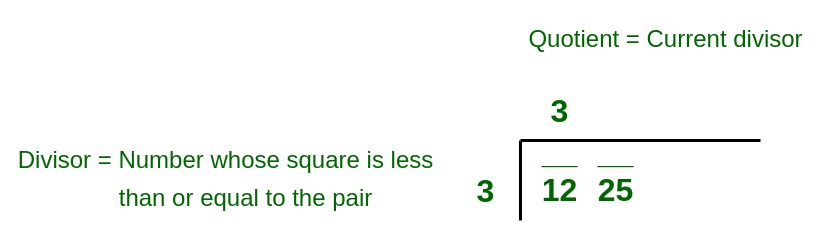
3. Subtract the square of the divisor from the first segment and bring down the next segment to the right of the remainder to get the new dividend.
For example:
12 - 9 = 3 is concatenated with next segment 25.
New dividend = 325

4. Now, the new divisor is obtained by taking two times the previous quotient(which was 3 in the above example as 32 = 9) and concatenating it with a suitable digit which is also taken as the next digit of the quotient, chosen in such a way that the product of the new divisor and this digit is equal to, or just less than the new dividend.
For example:
Two times quotient 3 is 6.
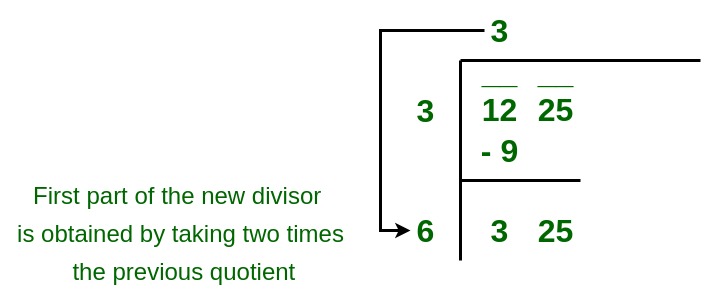
65 times 5 is 325 which is closest to the new dividend.
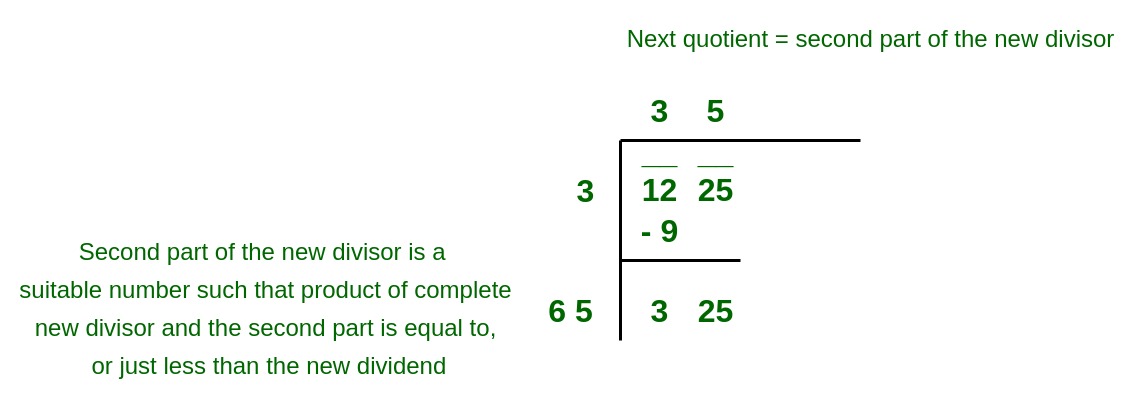
5. Repeat steps (2), (3) and (4) till all the segments have been taken up. Now, the quotient so obtained is the required square root of the given number.
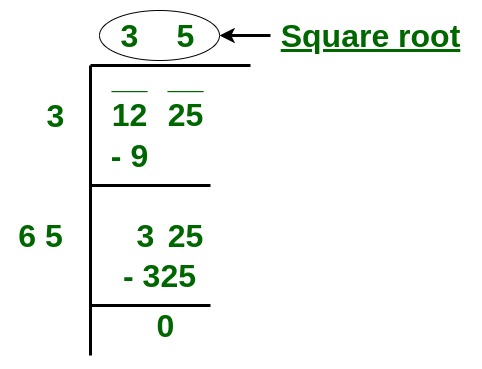
Below is the implementation of the above approach:
CPP
#include <bits/stdc++.h>
using namespace std;
#define INFINITY_ 9999999
int sqrtByLongDivision(int n)
{
int i = 0, udigit, j;
int cur_divisor = 0;
int quotient_units_digit = 0;
int cur_quotient = 0;
int cur_dividend = 0;
int cur_remainder = 0;
int a[10] = { 0 };
while (n > 0) {
a[i] = n % 100;
n = n / 100;
i++;
}
i--;
for (j = i; j >= 0; j--) {
cur_remainder = INFINITY_;
cur_dividend = cur_dividend * 100 + a[j];
for (udigit = 0; udigit <= 9; udigit++) {
if (cur_remainder >= cur_dividend
- ((cur_divisor * 10 + udigit)
* udigit)
&& cur_dividend
- ((cur_divisor * 10 + udigit) * udigit)
>= 0) {
cur_remainder = cur_dividend - ((cur_divisor * 10
+ udigit)
* udigit);
quotient_units_digit = udigit;
}
}
cur_quotient = cur_quotient * 10
+ quotient_units_digit;
cur_divisor = cur_quotient * 2;
cur_dividend = cur_remainder;
}
return cur_quotient;
}
int main()
{
int x = 1225;
cout << sqrtByLongDivision(x) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG{
static final int INFINITY_ =9999999;
static int sqrtByLongDivision(int n)
{
int i = 0, udigit, j;
int cur_divisor = 0;
int quotient_units_digit = 0;
int cur_quotient = 0;
int cur_dividend = 0;
int cur_remainder = 0;
int a[] = new int[10];
while (n > 0) {
a[i] = n % 100;
n = n / 100;
i++;
}
i--;
for (j = i; j >= 0; j--) {
cur_remainder = INFINITY_;
cur_dividend = cur_dividend * 100 + a[j];
for (udigit = 0; udigit <= 9; udigit++) {
if (cur_remainder >= cur_dividend
- ((cur_divisor * 10 + udigit)
* udigit)
&& cur_dividend
- ((cur_divisor * 10 + udigit) * udigit)
>= 0) {
cur_remainder = cur_dividend - ((cur_divisor * 10
+ udigit)
* udigit);
quotient_units_digit = udigit;
}
}
cur_quotient = cur_quotient * 10
+ quotient_units_digit;
cur_divisor = cur_quotient * 2;
cur_dividend = cur_remainder;
}
return cur_quotient;
}
public static void main(String[] args)
{
int x = 1225;
System.out.print(sqrtByLongDivision(x) +"\n");
}
}
|
Python3
INFINITY_ = 9999999
def sqrtByLongDivision(n):
i = 0
udigit, j = 0, 0
cur_divisor = 0
quotient_units_digit = 0
cur_quotient = 0
cur_dividend = 0
cur_remainder = 0
a = [0]*10
while (n > 0):
a[i] = n % 100
n = n // 100
i += 1
i -= 1
for j in range(i, -1, -1):
cur_remainder = INFINITY_
cur_dividend = cur_dividend * 100 + a[j]
for udigit in range(10):
if (cur_remainder >= cur_dividend
- ((cur_divisor * 10 + udigit)
* udigit)
and cur_dividend
- ((cur_divisor * 10 + udigit) * udigit)
>= 0):
cur_remainder = cur_dividend - ((cur_divisor * 10
+ udigit)
* udigit)
quotient_units_digit = udigit
cur_quotient = cur_quotient * 10 + quotient_units_digit
cur_divisor = cur_quotient * 2
cur_dividend = cur_remainder
return cur_quotient
x = 1225
print(sqrtByLongDivision(x))
|
C#
using System;
class GFG
{
static readonly int INFINITY_ =9999999;
static int sqrtBylongDivision(int n)
{
int i = 0, udigit, j;
int cur_divisor = 0;
int quotient_units_digit = 0;
int cur_quotient = 0;
int cur_dividend = 0;
int cur_remainder = 0;
int []a = new int[10];
while (n > 0) {
a[i] = n % 100;
n = n / 100;
i++;
}
i--;
for (j = i; j >= 0; j--) {
cur_remainder = INFINITY_;
cur_dividend = cur_dividend * 100 + a[j];
for (udigit = 0; udigit <= 9; udigit++) {
if (cur_remainder >= cur_dividend
- ((cur_divisor * 10 + udigit)
* udigit)
&& cur_dividend
- ((cur_divisor * 10 + udigit) * udigit)
>= 0) {
cur_remainder = cur_dividend - ((cur_divisor * 10
+ udigit)
* udigit);
quotient_units_digit = udigit;
}
}
cur_quotient = cur_quotient * 10
+ quotient_units_digit;
cur_divisor = cur_quotient * 2;
cur_dividend = cur_remainder;
}
return cur_quotient;
}
public static void Main(String[] args)
{
int x = 1225;
Console.Write(sqrtBylongDivision(x) +"\n");
}
}
|
Javascript
<script>
let INFINITY_ =9999999;
function sqrtByLongDivision(n)
{
let i = 0, udigit, j;
let cur_divisor = 0;
let quotient_units_digit = 0;
let cur_quotient = 0;
let cur_dividend = 0;
let cur_remainder = 0;
let a = new Array(10);
while (n > 0) {
a[i] = n % 100;
n = Math.floor(n / 100);
i++;
}
i--;
for (j = i; j >= 0; j--) {
cur_remainder = INFINITY_;
cur_dividend = cur_dividend * 100 + a[j];
for (udigit = 0; udigit <= 9; udigit++) {
if (cur_remainder >= cur_dividend
- ((cur_divisor * 10 + udigit)
* udigit)
&& cur_dividend
- ((cur_divisor * 10 + udigit) * udigit)
>= 0) {
cur_remainder = cur_dividend - ((cur_divisor * 10
+ udigit)
* udigit);
quotient_units_digit = udigit;
}
}
cur_quotient = cur_quotient * 10
+ quotient_units_digit;
cur_divisor = cur_quotient * 2;
cur_dividend = cur_remainder;
}
return cur_quotient;
}
let x = 1225;
document.write(sqrtByLongDivision(x) +"<br>");
</script>
|
Time Complexity: O((log100n)2 * 10)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...