If the side of a square is 10 cm then how many times will the new perimeter become if the side length is doubled?

Square is a closed two-dimensional figure with four sides and four corners. The length of all four sides is equal and parallel to each other. The basic figure of a square is shown below.

A square is a quadrilateral in which:

• The opposite sides are parallel.
• All four sides are equal.
• All angles measure 90°.

Perimeter of the square

The length of the boundary of a square can be calculated by performing the summation of all its sides, which is given by, 

Perimeter of a square = side + side + side + side. 

Therefore, Perimeter of Square = (4 × Side) units

If the side of a square is 10 cm then how many times will the new perimeter become if the side length is doubled?

Solution:

Here we will be finding how many times the perimeter of a square will be changed if we double the sides of the square

Perimeter of a square = Side + Side + Side + Side

Perimeter of a square = 4 × Side

Here we have the side of the square = 10 cm

Putting the value of the side of square in the perimeter of a square formula

Perimeter of a square = 4 × 10

Perimeter of a square = 40 cm  ………….(1)

When the side of the square is doubled 

The side of the new square becomes 2 × 10 cm = 20 cm

Perimeter of the new square = 4 × Side

Perimeter of the new square = 4 × 20

Perimeter of the new square = 80 cm  ……….(2)

Now we will be finding the change in the perimeter after increasing the side of the square

Perimeter of the original square = 40 cm  (from 1)

Perimeter of the new square = 80 cm  (from 2)

To find the increase in the perimeter

Subtract (1) from (2)

Increase in Perimeter = Perimeter of the new square – Perimeter of the original square 

⇒ Increase in Perimeter = 80 – 40 

⇒ Increase in Perimeter = 40 cm

To find how many times the perimeter is increased

Increase in the perimeter =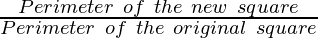 

Increase in the perimeter =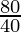 

Increase in the perimeter = 2 times

Therefore,

We can see that the perimeter of the new square is double the perimeter of the original square

Thus,

The perimeter of a square is increased by 2 times when its sides are doubled.

Similar Questions

Question 1. If the side of a square is 20 cm and its sides are tripled find how many times the new perimeter is increased?

Solution:

Here we have to find how many times the perimeter will be increased if the side of the square is tripled

As we know that

Perimeter of a square = 4 × side

Given : Side of the square is 20 cm

Perimeter of a square = 4 × 20

Perimeter of a square = 80 cm

Further,

When the side of the square is tripled

Side of the new square = 3 × 20

Side of the new square = 60 cm

Now,

Perimeter of the new square = 4 × side

Perimeter of the new square = 4 × 60

Perimeter of the new square = 240 cm

Further we will find the increase in perimeter

Increase in Perimeter = Perimeter of the new square – Perimeter of the original square 

Increase in Perimeter = 240 – 80

Increase in Perimeter = 160

To find how many times the perimeter is increased

Increase in the perimeter =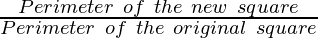 

Increase in the perimeter =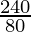 

Increase in the perimeter = 3 times

Therefore,

We can see that the perimeter of the new square is triple the perimeter of the original square

Thus,

The perimeter of a square is increased by 3 times when its sides are tripled.

Question 2. Find how many times the perimeter of a square will decrease if the side of the square is reduced by half. The side of the original square is 50 cm?

Solution:

Here we have to find how many times the perimeter will be reduced if the side of the square is halved.

As we know that

Perimeter of a square = 4 × side

Given: Side of the square is 50 cm

Perimeter of a square = 4 × 50

Perimeter of a square = 200 cm

Further,

When the side of the square is halved

Side of the new square =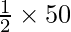 

Side of the new square = 25 cm

Now,

Perimeter of the new square = 4 × side

Perimeter of the new square = 4 × 25

Perimeter of the new square = 100 cm

Further we will find the decrease in perimeter

Increase in Perimeter = Perimeter of the original square – Perimeter of the new square

Decrease in Perimeter = 200 – 100

Decrease in Perimeter = 100 cm

To find how many times the perimeter is decreased 

 in the perimeter =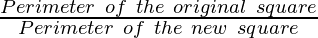 

Decrease in the perimeter =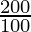 

Decrease in the perimeter = 2 times

Therefore,

We can see that the perimeter of the new square is reduced by 2 times the perimeter of the original square

Thus,

The perimeter of a square is reduced to half when its sides are halved.

Question 3. If the perimeter of a square is increased by four times, then find how many times the side of the new square is increased. The perimeter of the original square is 160 cm?

Solution:

Here we have to find the increase in the side of the square when its perimeter is increased by four times

As we know that

Perimeter of a square = 4 × side

Given: Perimeter of the original square is 160 cm

Perimeter of the original square = 160 cm

Perimeter of the original square = 4 × side

160 = 4 × side

Side = 

Side of the original square = 40 cm

Further,

Perimeter of the original square is increased by four times

Perimeter of the new square = 4 × 160

Perimeter of the new square = 640 cm

Perimeter of the new square = 4 × side

640 = 4 × side

Side =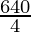 

Side = 160 cm

Side of the new square = 160 cm

Now,

Side of the original square = 40 cm

Side of the new square = 160 cm

Increase in side = Side of the new square – Side of the original square 

Increase in Perimeter = 160 – 40

Increase in Perimeter = 120 cm

To find how many times the side is increased

Increase in the side =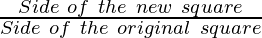 

Increase in the perimeter = 

Increase in the perimeter = 4 times

Therefore,

We can see that the side of the new square is increased by four times the side of the original square

Thus,

The side of a square is increased by four times when its perimeter is increased by four times.

Question 4. Find the perimeter of the square is its area is 25 cm²?

Solution:

Here we have to find the perimeter of the square by the given area.

Given: Area of the square is 25 cm².

As we know that

Area of the square = Side × Side

25 = s × s

s² = 25

s =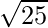 

s = 5 cm

Side of the square is 5 cm

Further,

Perimeter of the square = 4 × side

Perimeter of the square = 4 × 5

Perimeter of the square = 20 cm

Therefore,

Perimeter of the square is 20 cm if its area is 25 cm².

Question 5. If the side of a square is increased by 2 times, then find how many times the area of the new square will be. The side of the original square is 10 cm.

Solution:

Here we have to find how many times the area will be increased if the side of the square is doubled

As we know that

Area of a square = side × side

Given: Side of the square is 10 cm

Area of a square = 10 × 10

Area of a square = 100 cm²

Further,

When the side of the square is doubled

Side of the new square = 2 × 10

Side of the new square = 20 cm

Now,

Area of the new square = side × side

Area of the new square = 20 × 20

Perimeter of the new square = 400 cm²

Further we will find the increase in area

Increase in area = Area of the new square – Area of the original square

Increase in Area = 400 – 100

Increase in Area = 300

To find how many times the area is increased

Increase in the area =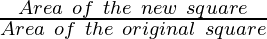 

Increase in the area =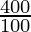 

Increase in the area = 4 times

Therefore,

We can see that the area of the new square is 4 times the area of the original square

Thus,

The area of a square is increased by 4 times when its sides are doubled.