The perimeter of any figure is defined as the sum of all its sides. In a simple way, we just need to add up all the sides to get the perimeter. In this article, we will deal with what is perimeter, how to find the perimeter of different types of triangles when one side is known, through some simple examples we will learn more about how we can calculate perimeter.
Perimeter of triangle = a + b+ c (Sum of all sides)
Where, a, b and c are lengths of each side. The unit of the perimeter is meter(m), centimeters(cm), or depending on the unit of length which is given to us.
Perimeter of triangle
As shown above, the perimeter of a triangle is the sum of the sides. Due to the different types of triangles, there are certain modifications in the formula to make them easy according to the type of triangle. Let’s take a look at the different types of formulae based on the different (Equilateral, isosceles, scalene) triangles.
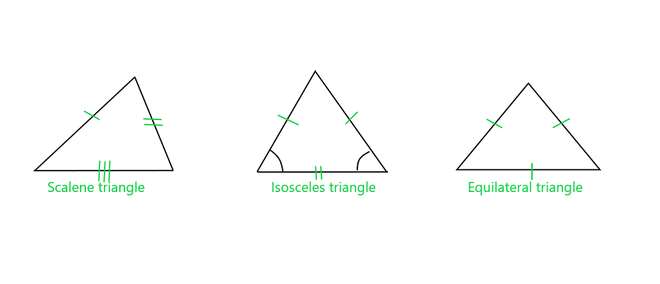
All kinds of triangle
- Perimeter of Scalene Triangle
Scalene Triangle is defined when all sides of a triangle are different, it is a scalene triangle. Let a, b, and c units be the sides of a triangle given now we know in a scalene triangle all are unequal so, the formula for the perimeter of a scalene triangle is,
Perimeter = a + b + c
- Perimeter of Isosceles Triangle
Isosceles Triangle is defined when two sides of a triangle are equal, it is an Isosceles triangle. Let a, b, and c units be the sides of a triangle given, now we know in Isosceles triangle two sides are equal (a = b) so, the formula for the perimeter of an Isosceles triangle is,
Perimeter = a + b + c = 2a + c
- Perimeter of Equilateral Triangle
An equilateral Triangle is defined as when the sides of all triangles are equal, it is an equilateral triangle. if a, b, and c units be the sides of a triangle given now we know in an equilateral triangle all sides are equal so, the formula for the perimeter of a scalene triangle is,
Perimeter = a + b + c = 3 × a
Steps to Calculate the Perimeter of a Triangle
The perimeter of any triangle can be calculated with the following steps:
- Step 1: The measurements of all the sides of a triangle should be in the same units.
- Step 2: Calculate the sum of all the sides.
- Step 3: after that end up answering along with its unit.
Let us take an example of how to calculate perimeter,
Example: Find the perimeter of △ABC having the following dimensions: AB = 3 cm, BC = 5 cm and AC = 7 cm.
Solution:
Simply, Perimeter of triangle ABC = AB + BC + AC
= 3 + 5 + 7
= 15 cm.
Finding the perimeter of a triangle with only one side
Let’s take a look at the different concepts of finding the perimeter of the triangle when only one side of the triangle and the angles are provided. The law is known as the Law of sines,
Law of sines formula
Given: △ABC
AB = c, BC = a and AC = b.
Construct a perpendicular line to CD from AB, CD ⊥ AB. Then CD = h (height of triangle), h separates the △ ABC in two right-angled triangles, △CDA and △CDB.

To Prove: a / b = Sin A / Sin B
Proof: In the △CDA,
Sin A = h/b (Sin ∅ = perpendicular/ hypotenuse)
Now In, △CDB,
Sin B = h/a
Therefore,
Sin A / Sin B = (h / b) / (h / a)
= a / b
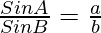
Hence Proved.
Similarly, 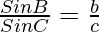 and similar for any pair of angles and their opposite sides.
and similar for any pair of angles and their opposite sides.
Sample Problems
Question 1: Find the perimeter of the triangle with the sides given as 12cm, 20cm, and 9cm.
Solution:
Given,
Sides of triangle are as: 12cm, 20cm, 9cm.
Perimeter of triangle = sum of all the sides
= 12 + 20 + 9
= 41 cm
Question 2: Check if the triangle is valid or not if the sides are: 12cm, 6cm, and 3cm.
Solution:
A valid triangle is defined as if sum of its two sides is greater than the third one for each side this rule should obey.
- a + b > c
- a + c > b
- b + c > a
In the given question we have: 12cm, 6cm and 3cm as sides of triangle
6 + 3 < 12 which does not obey condition, therefore this cannot be valid triangle’s dimensions.
Question 3: An isosceles triangle has a perimetеr of 37 m and its base has a length of 9 m calculate other sides.
Solution:
Perimeter of triangle = 37 m
Perimeter of isosceles triangle = 37 m
2a + c = 37
2 × 9 + c = 37
c = 37 – 18
c = 19 m
Other two sides are 19 and 19 m respectively
Question 4: If the height of the triangle is 8cm and the base is 4cm calculate its Area.
Solution:
Given:
Height of triangle = 8cm
Base of triangle = 4cm
Area of triangle = 1/2 × base × height
= 1/2 × 8 × 4
= 16 cm2
Question 5: If two angles of a triangle are 45° then calculate the third angle and also the type of triangle.
Solution:
First two angles are = 45°
We know that the sum of interior angle of triangle = 180°
∠1 + ∠ 2 + ∠3 = 180°
45° + 45° + ∠3 = 180° = > ∠3 = 180 ° – 90°
∠3 = 90°
We have an angle equal to right angle this shows that type of triangle is Right angles triangle.
Question 6: Perimeter of an equilateral triangle is 18cm calculate its area.
Solution:
Given,
Perimeter of Equilateral triangle = 18cm
3 × side = 18
Side = 18/3 = 6
Area of equilateral triangle = √3/4 side2 = √3/4 × 6 × 6
= 9√3 cm2
Question 7: Calculate the Perimeter of a triangle with only one side given and the angles are as 105°, 45°, and 30° and side given is 8 units, which is opposite of 30°.
Solution:
Let a be the length of the side opposite the 45∘ angles, b the length of the side opposite the 105° angle.
The Law of Sines is as,
8 / sin(30°) = a / sin(45°) = b / sin(105°)
sin(30°) = 0.5
sin(45°) = 0.707107
sin(105°) = 0.965926
8 / sin (30°) = 16
a = 16 × sin(45°) = 11.3137
b = 16 × sin(105°) = 15.4542
Perimeter = 8 + a + b
= 34.76852
Share your thoughts in the comments
Please Login to comment...