How to Compute a Discrete-Fourier Transform Coefficients Directly in Java?
Last Updated :
08 Sep, 2022
The Discrete Fourier Transform (DFT) generally varies from 0 to 360. There are basically N-sample DFT, where N is the number of samples. It ranges from n=0 to N-1. We can get the co-efficient by getting the cosine term which is the real part and the sine term which is the imaginary part.
The formula of DFT:
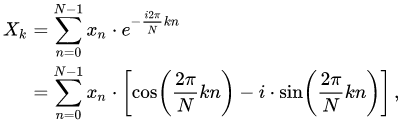
Example :
Input:
Enter the values of simple linear equation
ax+by=c
3
4
5
Enter the k DFT value
2
Output:
(-35.00000000000003) - (-48.17336721649107i)
Input:
Enter the values of simple linear equation
ax+by=c
2
4
5
Enter the k DFT value
4
Output:
(-30.00000000000001) - (-9.747590886987172i)
Approach:
- First, let us declare the value of N is 10
- We know the formula of DFT sequence is X(k)= e^jw ranges from 0 to N-1
- Now we first take the inputs of a, b, c, and then we try to calculate in “ax+by=c” linear form
- We try to take the function in an array called ‘newvar’.
newvar[i] = (((a*(double)i) + (b*(double)i)) -c);
- Now let us take the input variable k, and also declare sin and cosine arrays so that we can calculate real and imaginary parts separately.
cos[i]=Math.cos((2*i*k*Math.PI)/N);
sin[i]=Math.sin((2*i*k*Math.PI)/N);
- Now let us take real and imaginary variables
- Calculating imaginary variables and real variables like
real+=newvar[i]*cos[i];
img+=newvar[i]*sin[i];
- Now we will print this output in a+ ib form
Implementation:
Java
import java.io.*;
import java.util.Scanner;
class GFG {
public static void main(String[] args)
{
int N = 10;
System.out.println(
"Enter the values of simple linear equation");
System.out.println("ax+by=c");
double a = 3.0;
double b = 4.0;
double c = 5.0;
double[] newvar = new double[N];
for (int i = 0; i < N; i++) {
newvar[i]
= (((a * (double)i) + (b * (double)i)) - c);
}
System.out.println("Enter the k DFT value");
int k = 2;
double[] cos = new double[N];
double[] sin = new double[N];
for (int i = 0; i < N; i++) {
cos[i] = Math.cos((2 * i * k * Math.PI) / N);
sin[i] = Math.sin((2 * i * k * Math.PI) / N);
}
double real = 0, img = 0;
for (int i = 0; i < N; i++) {
real += newvar[i] * cos[i];
img += newvar[i] * sin[i];
}
System.out.println("(" + real + ") - "
+ "(" + img + "i)");
}
}
|
Output
Enter the values of simple linear equation
ax+by=c
Enter the k DFT value
(-35.00000000000003) - (-48.17336721649107i)
Time complexity: O(n)
Auxiliary space: O(n) for array
Share your thoughts in the comments
Please Login to comment...