Generate an alternate odd-even sequence having sum of all consecutive pairs as a perfect square
Last Updated :
26 Nov, 2021
Given an integer N, the task is to print a sequence of length N consisting of alternate odd and even numbers in increasing order such that the sum of any two consecutive terms is a perfect square.
Examples:
Input: N = 4
Output: 1 8 17 32
Explanation:
1 + 8 = 9 = 32
8 + 17 = 25 = 52
17 + 32 = 49 = 72
Input: N = 2
Output: 1 8
Approach: The given problem can be solved based on the observation from the above examples, that for an integer N, sequence will be of the form 1, 8, 17, 32, 49 and so on. Therefore, the Nth term can be calculated by the following equation:
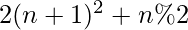
Therefore, to solve the problem, traverse the range [1, N] to calculate and print every term of the sequence using the above formula.
Below is the implementation of the above approach:
C++
#include <iostream>
using namespace std;
void findNumbers(int n)
{
int i = 0;
while (i <= n) {
cout << 2 * i * i + 4 * i
+ 1 + i % 2
<< " ";
i++;
}
}
int main()
{
int n = 6;
findNumbers(n);
}
|
Java
import java.util.*;
class GFG{
static void findNumbers(int n)
{
int i = 0;
while (i <= n)
{
System.out.print(2 * i * i + 4 * i +
1 + i % 2 + " ");
i++;
}
}
public static void main (String[] args)
{
int n = 6;
findNumbers(n);
}
}
|
Python3
def findNumbers(n):
i = 0
while (i <= n):
print(2 * i * i + 4 * i +
1 + i % 2, end = " ")
i += 1
n = 6
findNumbers(n)
|
C#
using System;
class GFG{
static void findNumbers(int n)
{
int i = 0;
while (i <= n)
{
Console.Write(2 * i * i + 4 * i +
1 + i % 2 + " ");
i++;
}
}
public static void Main ()
{
int n = 6;
findNumbers(n);
}
}
|
Javascript
<script>
function findNumbers(n)
{
var i = 0;
while (i <= n) {
document.write(2 * i * i + 4 * i + 1 + i % 2+" ");
i++;
}
}
var n = 6;
findNumbers(n);
</script>
|
Output: 1 8 17 32 49 72 97
Time Complexity: O(N)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...