Find the equation for the ellipse with center at (0,4), focus at (8,4), and vertex at (6, 7)
Last Updated :
15 Feb, 2023
Conic sections, commonly known as conics, are created when a plane intersects a cone. The angle at which these sections intersect determines their geometry. Conic sections are therefore classified into four types: circle, ellipse, parabola, and hyperbola. Each of these types is distinguished by its unique set of mathematical properties and equations. The ellipse is explained more below.
Ellipse
An ellipse is a conic section generated when a plane crosses a cone at an angle (β) smaller than the right angle but greater than the angle formed at the cone’s vertex (α). In other terms, an ellipse is generated when a plane slices a cone at an angle β such that α<β<90o.

As illustrated in the image above, a cone and a plane cross at an angle that is less than the right angle but more than the angle formed at the vertex of the cone to create an ellipse as a result of the intersection.
Equation of an ellipse
- The standard equation of an ellipse centered at (h, k) with a major axis parallel to the x-axis is given by:
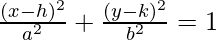 ,
,
where the coordinates of the vertex are (h±a, 0), coordinates of co-vertex are (h, k±b) and the coordinates of foci are (h±c, k), where c2 = a2 – b2.

Horizontal ellipse
- The standard equation of an ellipse centered at (h, k) with a major axis parallel to the y-axis is given by:
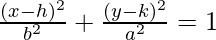 ,
,
where the coordinates of the vertex are (h, k±a), coordinates of co-vertex are (h±b, k) and the coordinates of foci are (h, k±c), where c2 = a2 – b2.

Vertical ellipse
Find the equation for the ellipse with center at (0,4), focus at (8,4), and vertex at (6, 7).
Solution:
To find the equation of an ellipse, we need the values a and b.
The distance between the center (0, 4) and the focus (8, 4) gives c.
So, c2 = (8 – 0)2 + (4 – 4)2
c2 = 64
The distance between the center (0, 4) and the vertex (6, 7) gives a.
So, a2 = (6 – 0)2 + (7 – 4)2
a2 = 36 + 9
a2 = 45
Put the obtained values in the formula c2 = a2 – b2 to find b.
b2 = 64 – 45
b2 = 19
As the y-coordinates of center and focus are same, ellipse lies on x-axis. So the equation is of the form 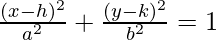
Hence the required equation of the ellipse is, 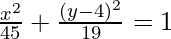
Similar Problems
Question 1. Find an equation for the ellipse lying on the y-axis with centre at (0,7), length of major axis 12 units, and length of minor axis 16 units.
Solution:
The length of major axis is, 2a = 12 => a = 6.
The length of minor axis is, 2b = 16 => b = 8.
As the ellipse lies on y-axis, the equation is 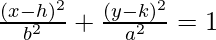
So, the equation is 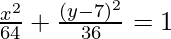 .
.
Question 2. Find an equation for the ellipse lying on the x-axis with center at (3,2), length of major axis 2 units, and length of minor axis 8 units.
Solution:
The length of major axis is, 2a = 2 => a = 1.
The length of minor axis is, 2b = 8 => b = 4.
As the ellipse lies on x-axis, the equation is 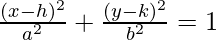
So, the equation is 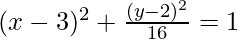 .
.
Question 3. Find the coordinates of the major axis of the ellipse with foci (0, 6) and minor axis (8, 0).
Solution:
We have, c = 6 and b = 8.
Put these in c2 = a2 – b2 to find a.
a2 = 62 + 82
a2 = 100
a = 10
The coordinates of major axis are (0, ±10).
Question 4. Find the equation of an ellipse centered at (7, 2) with c = 3 and b = 4.
Solution:
Given b = 4, c = 3, h = 7 and k = 2.
Put these in the formula c2 = a2 – b2 to find a.
a2 = 42 + 32
a2 = 25
a = 5
As the ellipse lies on x-axis, the equation is of the form 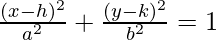
So, the equation is, 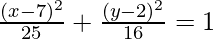
Question 5. Find the equation of the ellipse centered at the origin if a = 12, b = 6, and the minor axis is parallel to the x-axis.
Solution:
The minor axis is parallel to x-axis, so the ellipse lies on y-axis.
The equation is of the form 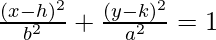 .
.
Here a = 12 and b = 6, h = 0 and k = 0.
So, the equation becomes,
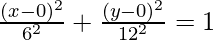
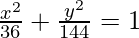
Share your thoughts in the comments
Please Login to comment...