Find the common difference of the AP 1/3, (1-3b)/3, (1-6b)/3, …

Arithmetic is known as the most basic part of number theory, which deals with numbers and the calculations concerning them. Operations such as addition, subtraction, multiplication, division are called arithmetic operations. These are +,-,*,/ are commonly used in daily lives. The addition is used to find the sum. Represented by ‘+’, Subtraction is used to find the difference. Represented by ‘-‘, Multiplication is used to find the product. Represented by ‘×’, The division is used to find the quotient Represented by ‘÷ ‘.

Sequence and Series

An organized collection of components in which reiterations of any kind are permitted is known as a sequence. Series is the sum of all the elements. Series is basically the sum of all terms of any sequence.

Arithmetic Progression

An arithmetic progression or sequence is a series/sequence of numbers such that the common difference between the consecutive terms remains constant i.e each term differs by the previous term (if exits) by a constant value. The common difference is denoted as “d”. If the sequence is, a₁, a₂, a₃, a₄, a₅,… a_n. The common difference becomes, 

d= a₂– a₁= a₃– a₂= a₄– a₃= a_n– a_n-1

Calculate the common difference of the A.P.  1/3, (1-3b)/3, (1-6b)/3.

Given that the three terms are in AP.

The given terms of AP :

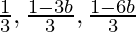
Now to get common differences, subtract the 1st term from the 2nd term.

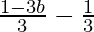
= -b

Hence the common difference is  -b. 

Similar Question

Question 1: Calculate the common difference of the A.P. ⇢ 2/9, (1-3b)/9, (1-6b)/9.

Solution:

Given that the three terms are in AP.

The given terms of AP :

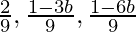
Now to get common differences, subtract the 1st term from the 2nd term.

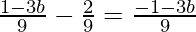
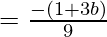
Hence the common difference is  .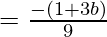 

Question 2: If 1, 6, 11, 16, 21… is an Arithmetic sequence, Find the Common difference.

Solution:

Given the elements are in AP.

Now to get common differences, subtract the 1st term from the 2nd term.

common difference = 6-1 = 5.

Hence the common difference is 5.

Question 3: If 1, 6,11,16, 21… is an Arithmetic sequence, Find the 100th term

Solution:

The nth term of an AP is given by : T_n  = a + (n-1)d,

where,

a is the first term

here a =1

d is the common difference.

here d= 6-1=5.

T_n = 1 + (100 – 1)5 = 496.

Hence the 100th term is 496.

Question 4: In an AP the 12th term is 36. If the first term is 3, Find the common difference of the AP.

Solution:

The nth term of an AP is given by: T_n  = a + (n-1)d,

where:

a is the first term

here a =3

n is the term 

here n = 12

T_n= nth term 

here T_n =36

d is the common difference.

Applying T_n  = a + (n-1)d 

36 = 3 + (12– 1)d 

d=3.

Hence the common difference is 3.