Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x2)/4 + (y2)/9 = 1
Last Updated :
28 Nov, 2022
Conic Sections is a branch of mathematics with deals with curves like a circle, parabola, ellipse, hyperbola, etc. These curves are also known as conic sections or conics because they can be obtained as intersections of a plane with a double-napped right circular cone. A circle, parabola, ellipse, etc. are obtained when a cone is cut in a certain way by a plane.
So, let’s discuss how we find the largest rectangle in an ellipse for the general equation:
General form of equation of ellipse: x2/a2 + y2/b2 = 1
So, let’s assume a point on the ellipse (acosθ, bsinθ) then the diagram will be:
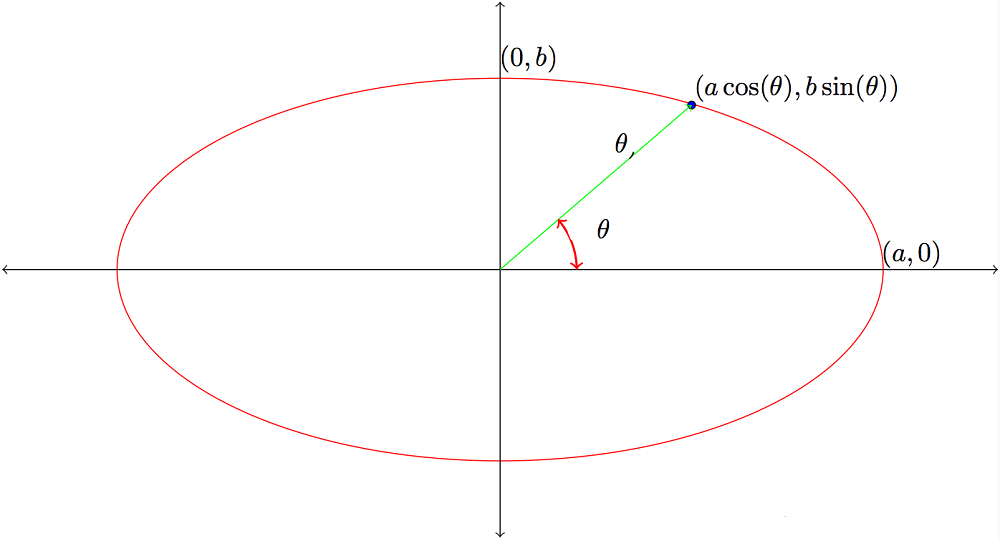
Now if rectangle we made a rectangle in ellipse it will be symmetric in both the x-axis and y-axis then the length and width of the rectangle will be:
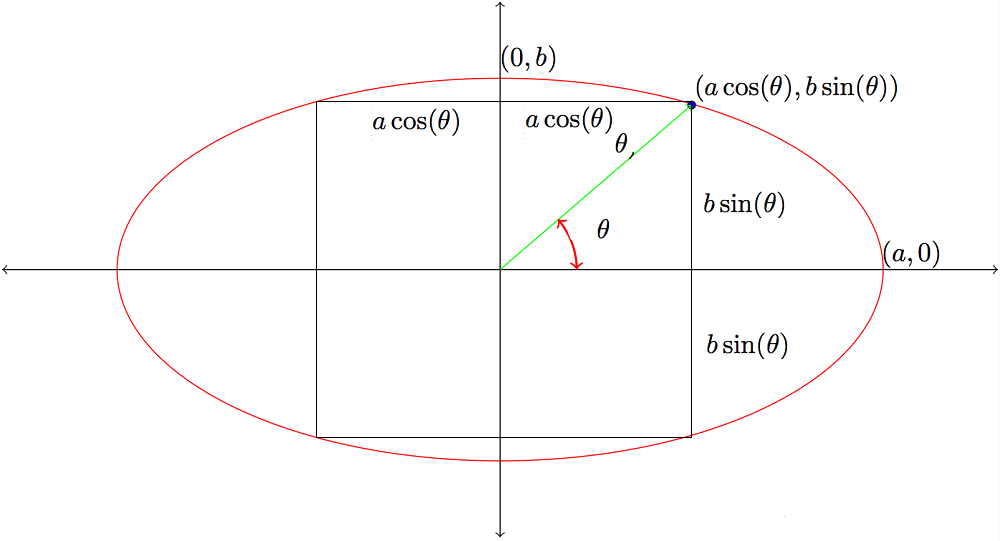
Then, from above diagram:
Length of Rectangle = 2acosθ
Width of Rectangle = 2bsinθ
Now the area of rectangle = length * width
A = 2acosθ * 2bsinθ
A = 2ab (2cosθsinθ) {Since sin2θ = 2cosθsinθ}
A = 2ab sin2θ
But we have to maximize the area so that we get the largest area of rectangle. For this we to calculate first order derivative of above equation and the equate to 0.
dA/dθ = d(2ab sin2θ)/dθ
dA/dθ = 2ab (2cos2θ)
dA/dθ = 4abcos2θ
Equating equation to 0 we get
4abcos2θ = 0
cos2θ = 0
2θ = π/2
θ = π/4
Now to check whether on this angle the area of the rectangle is maximum or minimum we have to again calculate differentiation of equation:-
d(dA/dθ)/dθ = d(4abcos2θ)/dθ
d2A/dθ2 = 4ab (-2sin2θ)
since, d2A/dθ2 < 0 i.e. second-order derivative is negative
Since the second-order derivative is negative therefore the given angle is maxima angle, and the value at this angle is maximum.
Therefore the area of the largest rectangle is A = 2ab sin2(π/4)
Area of largest Rectangle = 2ab
where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse.
Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x2)/4 + (y2)/9 = 1.
Solution:
Now in given equation we have equation of ellipse:
x2/4 + y2/9 = 1
On comparing with the general equation of ellipse:
x2/a2 + y2/b2 = 1
We get a = 2 and b = 3
As we know that the area of largest rectangle is 2ab
So, A = 2* 2 * 3
Area of largest rectangle that can be inscribed in given ellipse = 12
Similar Question
Question 1: Find the area of the largest rectangle that can be inscribed in the ellipse (x2/100) + (y2/64) = 1
Solution:
Formulae of the area of largest rectangle = 2ab
Here a = 10 and b = 8
Area = 2 * a * b
Area = 2 * 10 * 8
Area = 160 sq. units
Question 2: Find the area of the largest rectangle that can be inscribed in the ellipse (x2/36) + (y2/8) = 1
Solution:
Formulae of the area of largest rectangle = 2ab
Here a = 6 and b = √8 = 2√2
Area = 2 * a * b
Area = 2 * 6 * 2√2
Area = 24√2 sq. units
Question 3: Find the area of the largest rectangle that can be inscribed in the ellipse (x2/1) + (y2/9) = 1
Solution:
Formulae of the area of largest rectangle = 2ab
Here a = 1 and b = 3
Area = 2 * a * b
Area = 2 * 1 * 3
Area = 6 sq. units
Question 4: Find the area of the largest rectangle that can be inscribed in the ellipse (y2/400) + (x2/169) = 1
Solution:
Formulae of the area of largest rectangle = 2ab
Here a = 13 and b =20
Area = 2 * a * b
Area = 2 * 13 * 20
Area = 520 sq. units
Question 5: Find the area of the largest rectangle that can be inscribed in the ellipse (y2/18) + (x2/49) = 1
Solution:
Formulae of the area of largest rectangle = 2ab
Here a = 7 and b = √18 = 3√2
Area = 2 * a * b
Area = 2 * 7 * 3√2
Area = 42√2 sq. units
Share your thoughts in the comments
Please Login to comment...